La résistance électrique – Cours & Projets

Domaines d’applications

Circuits électriques
Filtres actifs/passifs
Alimentation réglable
Convertisseur N/A
Mesure du courant (shunt)
Capteurs résistifs
Résistance de démarrage

Caractéristiques d’une résistance

Un résistor linéaire (ou « résistance ») est caractérisé par : La résistance nominale (en ohms) : c’est la valeur indiquée par le constructeur sur le composant (à l’aide d’un code de couleurs, sauf pour les résistances de puissance, de précision, ou dans le cas de certains modèles spéciaux dont le marquage est effectué en clair).

La tolérance (en %) : nul constructeur ne peut assurer que la valeur qu’il inscrit sur un élément résistif est exactement égale à sa valeur réelle. Il est toutefois légalement tenu d’indiquer une fourchette de valeurs extrêmes entre lesquelles doit se trouver la valeur réelle de son composant. Cette fourchette est indiquée sous forme d’un pourcentage nommé tolérance de fabrication. La tolérance est également indiquée à l’aide d’un anneau de couleur ; elle fixe l’écart maximal entre la résistance nominale et la résistance effective du composant. Il existe des séries de valeurs normalisées associées à des tolérances données (voir page 2).

La puissance nominale (en watts) correspond à la puissance normale que peut dissiper la résistance à une température donnée (dans des conditions d’aération spécifiées). Si on demande à une résistance de dissiper une puissance trop importante elle peut :

Soit brûler
Soit, plus insidieusement, changer fortement de valeur sans modification de son aspect externe

Il est donc important de savoir calculer la puissance dissipée par une résistance dans un montage, et de choisir en fonction le bon type de résistance. La stabilité caractérise l’évolution relative de la résistance effective du composant, dans le temps. Une résistance stable ne changera pas de valeur en « vieillissant ». Le coefficient en température définie la sensibilité de la résistance par rapport à la température. Une résistance dont la valeur ne varie pas en fonction de la température aura un coefficient de température nul. Le coefficient de température est exprimé en °C-1, et il est défini par l’expression suivant : R=R0.(1+α.T), avec :

R = la valeur de la résistance en ohm
R0=la valeur de la résistance à 0°C en ohm
α=le coefficient en température en °C-1
T=la température en °C

Séries de valeurs normalisées

Une série définit une liste de valeurs nominales de la résistance, auxquels on applique un coefficient multiplicateur puissance de 10 (de 10-2 à 106). Par exemple, dans la série E6, il existe 6 valeurs normalisées, qui sont 10, 15, 22, 33, 47, et 68. Associées à un coefficient multiplicateur, ces valeurs normalisées peuvent donner les valeurs de résistances suivantes, toutes présentent dans la série E6 : 100kΩ, 150Ω, 15kΩ, 2.2MΩ, 3.3kΩ, 33kΩ, 470Ω, 68Ω,
680Ω, 6,8 kΩ, 68 kΩ, 680 kΩ, 6,8 MΩ, etc …

En revanche, les valeurs suivantes n’existent pas dans la série E6 : 120kΩ, 200Ω, 3.9Ω, 56Ω, car les valeurs normalisées 12, 20, 39, et 56 ne sont pas présentent dans la série E6. Pour obtenir ces valeurs de résistance il faudra utiliser une autre série de valeurs normalisées : E12 (avec 12 valeurs) ou E24 (avec 24 valeurs). Chaque série de valeurs normalisées possède :

Un nombre définit de valeurs normalisées (indiqué dans le nom de la série)
Une tolérance de la valeur réelle da la résistance par rapport à sa valeur nominale

Caractéristiques des principales séries de valeurs normalisées :

Série	E3	E6	E12	E24	E48	E96	E192
Nombre de valeurs	3	6	12	24	48	96	192
Nombre de chiffres significatifs	2	2	2	2	3	3	3
Tolérance	± 30 %	± 20 %	± 10 %	± 5 %	± 2 %	± 1 %	± 0,5 % ± 0,1 % ± 0,01 %

Voici les 6 valeurs de la série normalisée E6 :

Voici les 12 valeurs de la série normalisée E12 :

Voici les 24 valeurs de la série normalisée E24 :

10	11	12	13	15	16	18	20	22	24	27	30
33	36	39	43	47	51	56	62	68	75	82	91

Lecture de la valeur d’une résistance et code des couleurs

Suivant la série dans laquelle une résistance est choisie, il faudra 2 ou 3 chiffres significatifs pour exprimer la valeur normalisée de la résistance (en plus du coefficient multiplicateur). Exemples :

dans la série E12, les valeurs normalisées vont de 10 à 82 ; 2 chiffres suffisent donc pour écrire cette valeur
dans la série E48, les valeurs normalisées vont de 105 à 953 ; il faudra alors 3 chiffres pour indiquer ces valeurs.

Une résistance de la série E12 sera donc marquée par 2 anneaux de couleurs exprimant la valeur normalisée de la résistance, 1 anneau de couleur indiquant le coefficient multiplicateur de cette valeur normalisée, et 1 anneau de couleur indiquant la tolérance de la résistance :

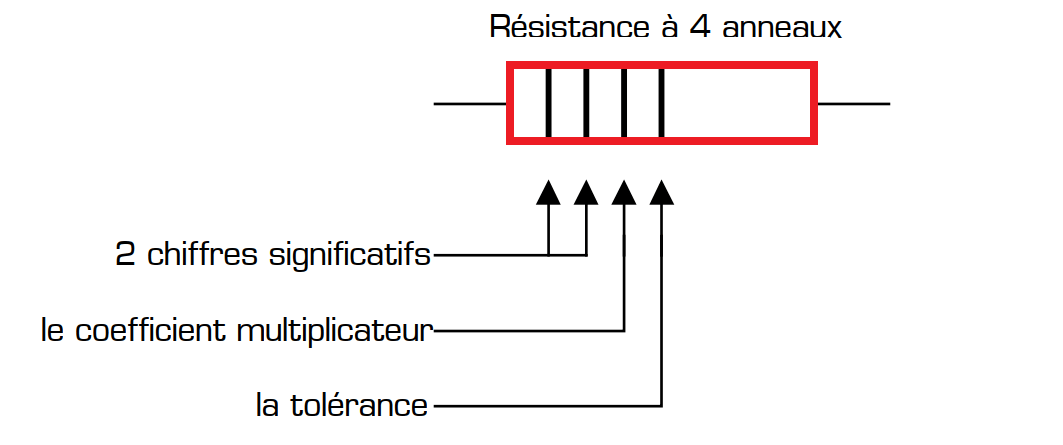
ne résistance de la série E48 sera marquée par 3 anneaux de couleurs exprimant la valeur normalisée de la résistance, 1 anneau de couleur indiquant le coefficient multiplicateur de cette valeur normalisée, et un 5ème anneau de couleur indiquant la tolérance :

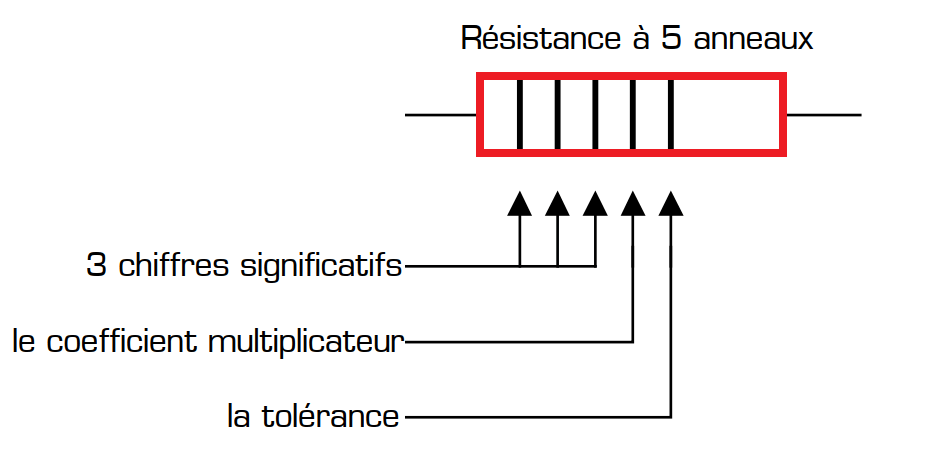
Le nombre d’anneaux de couleurs (4 ou 5 anneaux) inscrits sur une résistance dépend de la précision de la valeur normalisée de la résistance, et donc de série à laquelle appartient la résistance.

Code des couleurs :

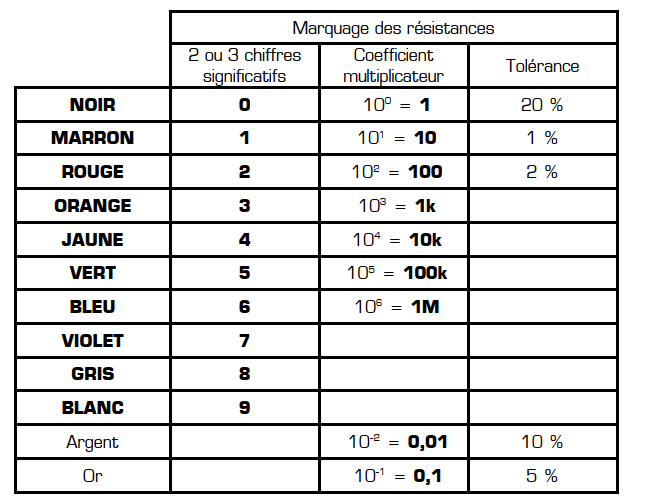
En pratique, le sens de lecture d’une résistance commence par le premier anneau situé le plus près de l’extrémité du corps. Pour les résistances ayant un anneau indiquant une tolérance (le plus souvent OR ou ARGENT), la lecture commence à l’opposée de celui-ci. De plus, l’anneau du coefficient multiplicateur peut être directement interprété comme « le nombre de zéros à ajouter après la valeur normalisée ».

Exemple : soit une résistance dont la valeur normalisée est 27 (1er anneau ROUGE et 2ème anneau VIOLET), et dont l’anneau indiquant le coefficient multiplicateur (le 3ème anneau) est ORANGE. Dans le code des couleurs, la couleur ORANGE exprime le chiffre 3 : il suffit donc d’ajouter 3 zéros à la valeur normalisée 27 pour obtenir la valeur nominale de la résistance. Notre résistance a donc une valeur de 27000Ω, soit 27kΩ.

Autre exemple : quelle est la couleur des anneaux sur une résistance de 680 kΩ ?

Réponse : 680 kΩ s’écrit 68 suivi de 4 zéros : il faut donc codé les chiffres 6, 8 et 4. Les anneaux peints sur une résistance de 680 kΩ seront donc de couleurs bleu (pour le 6), gris (pour le 8) et jaune (pour le 4). Voici 2 résistances dont les couleurs des anneaux sont données. Quelle est la valeur, et la tolérance, de
chacune de ces résistances ?

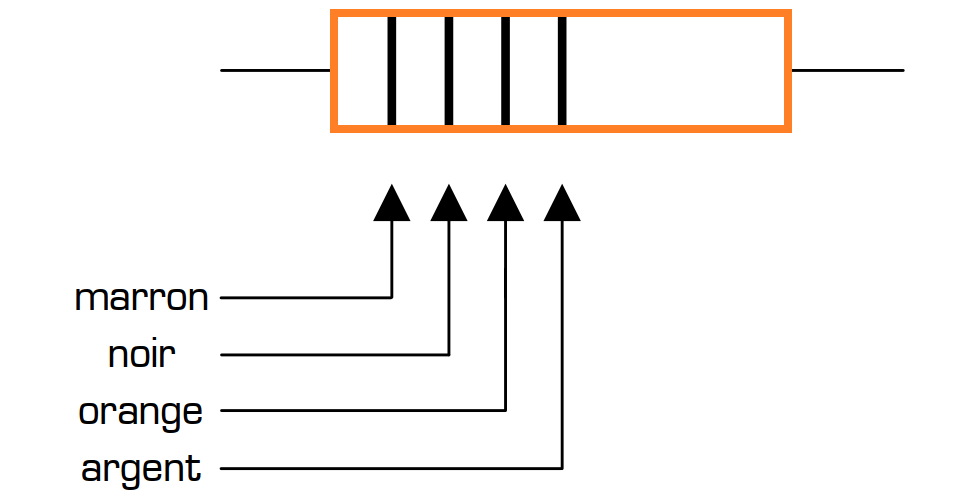
Réponse : marron=1 et noir=0, donc la valeur significative est 10 orange=3, il faut donc ajouter 3 zéros après la valeur significative, ce qui donne 10 000 Ω, soit 10 kΩ. L’anneau de la tolérance est de couleur argent, ce qui signifie que la tolérance est de 10 % (série E12) .

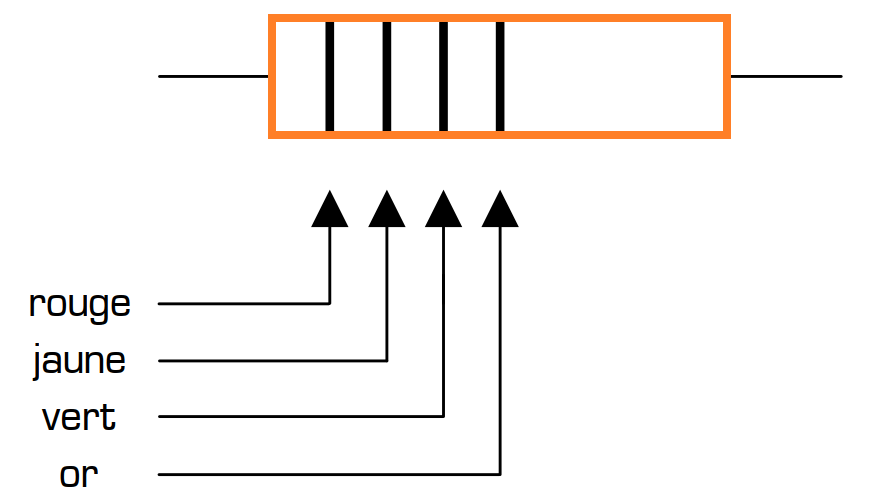
Réponse : rouge=2 et jaune=4, donc la valeur significative est 24 vert=5, il faut donc ajouter 5 zéros après la valeur significative, ce qui donne 24 00000 Ω, soit 2 400 kΩ, c’est-à-dire 2,4 MΩ. L’anneau de la tolérance est de couleur or, ce qui signifie que la tolérance est de 5 % (série E24) .

Les différentes technologies des résistances

Les conducteurs ohmiques ( ou « résistances ») utilisés en électronique se classent essentiellement en deux catégories : les résistances au carbone et les résistances métalliques.

Les résistances au carbone

Elles se divisent en 2 catégories :

Les résistances agglomérées constituées d’un mélange de carbone (substance conductrice), de matière isolante (silice …) et d’un liant (bakélite …). Tous ces constituants réduits en poudre sont agglomérés à chaud et isolés dans un tube de plastique ou de céramique. Le pourcentage de carbone détermine la valeur de la résistance. Peu coûteuses et robustes, les résistances agglomérées sont peu précises, et aujourd’huit leur construction est presque abandonnée.
Les résistances à couche de carbone obtenues en déposant une très mince couche de carbone sur un bâtonnet de céramique. Les extrémités du bâtonnet sont métalliques et le conducteur ohmique est protégé par un vernis ou un revêtement moulé. Le dosage plus ou moins dense de la poudre de carbone sur le bâtonnet de céramique isolant détermine entre les deux connexions extrêmes une résistance plus ou moins élevée. Les résistances à couche de carbone ont une stabilité et une précision moyenne, leur puissance nominale dissipée peut varier de 1/8 W à 2 W selon leurs dimensions, et elles sont de loin les résistances les plus répandues.

Les résistances métalliques

Elles se divisent aussi en 2 catégories :

Les résistances bobinées de puissance, constituées par un fil d’alliage (nichrome ou constantan) bobiné sur un support de céramique et moulé dans de l’émail. Elles permettent de réaliser des résistances étalons ou des résistances de puissances pouvant absorber jusqu’à 1kW. Pour réaliser des résistances de haute précision, de nombreuses précautions de fabrication doivent être prises : absence de contrainte mécanique sur le fil résistant lors du bobinage, mise en œuvre d’un traitement thermique de stabilisation pouvant durer plusieurs jours … On obtient alors des coefficients de température de l’ordre de 10-6 °C-1, et une stabilité voisine de 10-5 an-1 (soit une variation d’un ohm par an pour une résistance de 100 kΩ).
Les résistances à feuilles métalliques, sont des résistances de haute précision constituées d’une feuille en alliage (le plus souvent de nickel-chrome) fixée sur un substrat isolant (tube en verre ou en céramique) choisi pour ses qualités de stabilité et de bonne tenue en température.

Loi d’ohm

La loi d’Ohm est une loi physique empirique qui lie l’intensité du courant (I) électrique traversant un dipôle électrique à la tension (U) à ses bornes. Cette loi permet de déterminer la valeur d’une résistance (R). La loi d’Ohm a été ainsi nommée en référence au physicien allemand Georg Simon Ohm qui la publie en 1827, dans son œuvre Die galvanische Kette: mathematisch bearbeitet. Lire la suite…