Objectifs du projet électronique
- Etude et simulation numérique du filtre Moyenneur avec Matlab [1/3]
- Etude et simulation numérique du filtre Médiane avec Matlab [1/3]
- Etudes et simulation numérique des techniques de la détection de seuil [2/3]
- Etude comparatives et qualitative des méthodes [2/3]
- Implémentation sur microcontrôleur en utilisant le kit Arduino [3/3]
Etude et simulation numérique du filtre Moyenneur avec Matlab
Ce filtre lisseur part du principe que la valeur d’un signal est relativement similaire à son voisinage. Il fait donc en sorte que chaque valeur du signal est peut être remplacé par la moyenne pondérée de ses valeurs précédentes. Si on applique un filtre moyenneur de taille N=10, cela signifie qu’on additionne tous les valeurs précédentes de la valeur courante traitée puis on devise par la taille du filtre. On obtient ainsi la formule suivante du filtre.
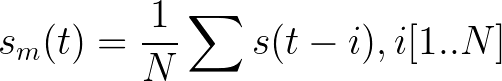
Exemple :
On considère un morceau du signal constitue de 10 échantillons passés, la valeur moyenne sur 10 échantillons à l’instant actuel correspond à l’application de formule ci-dessus.
s(t)=[10.2, 10, 10.5, 10.6, 10.4, 10.8,10.12,10,11], N=10
s_m(t) = (10.2+ 10+10.5+10.6+10.4+10.8+10.12+10+11)/10= 9.36
Etude de l’effet de la taille du filtre sur la qualité du signal
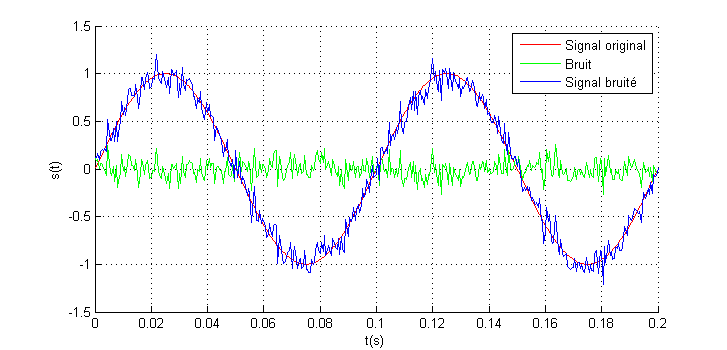
Pour comprendre le comportement du filtre et ses effets sur un signal. On va générer un signal sinusoïdal de fréquence Fo, puis ajouter un bruit gaussien de la moyenne mu et de la variance vare. Le signal bruité est l’addition du signal original et le bruit.
On va changer d’une façon linéaire la taille du filtre appliqué sur le signal bruite et ensuite le comparé avec le signal original.
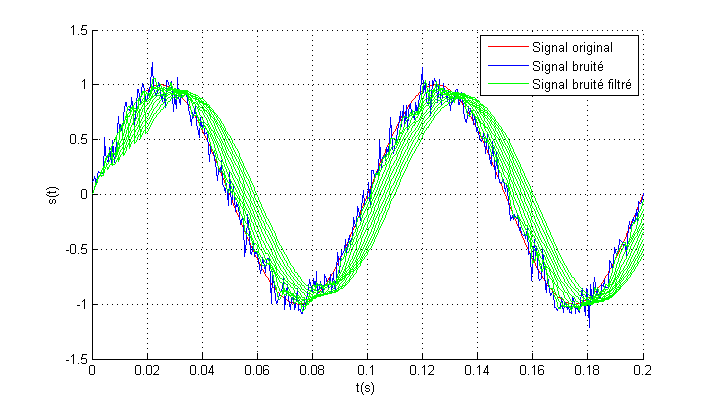
Bruit filtré pour N=40 & N=4
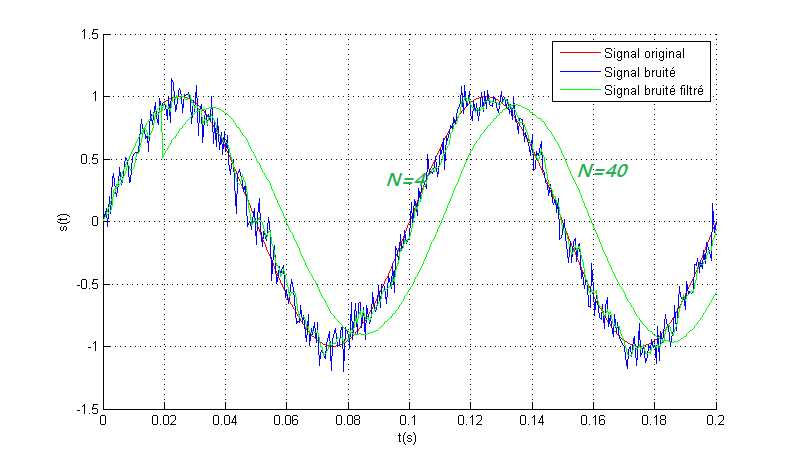
Bruit filtré pour N varié de 4 à 40 avec un pas de 4
L’Erreur Quadratique Moyenne EQM ou MSE (Mean Square Error)
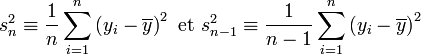
L’erreur quadratique moyenne (Mean Squared Error en anglais) est l’espérance du carré de l’erreur entre la vraie valeur et sa valeur estimée.
En topométrie, on emploie plus généralement l’abrégé “EQM” pour “erreur quadratique moyenne ”.
Soit un certain nombre de mesures. Chacune de ces mesures est entachée d’une erreur (rien à voir avec une faute) On appelle erreur vraie pour une mesure la différence entre la mesure et sa vraie valeur. Si cette même valeur a été mesurée plusieurs fois, on appelle erreur apparente d’une mesure isolée, la différence entre la moyenne arithmétique des mesures et la mesure isolée [Wiki].
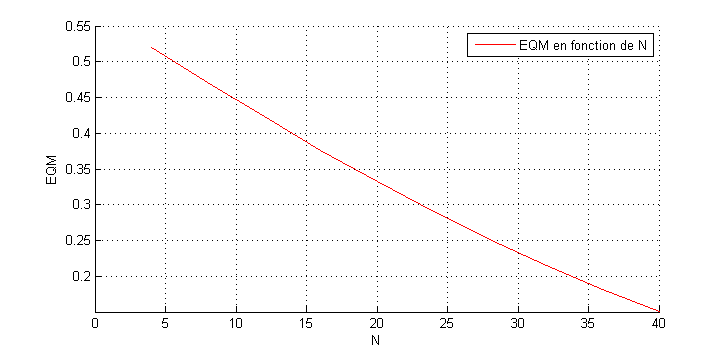
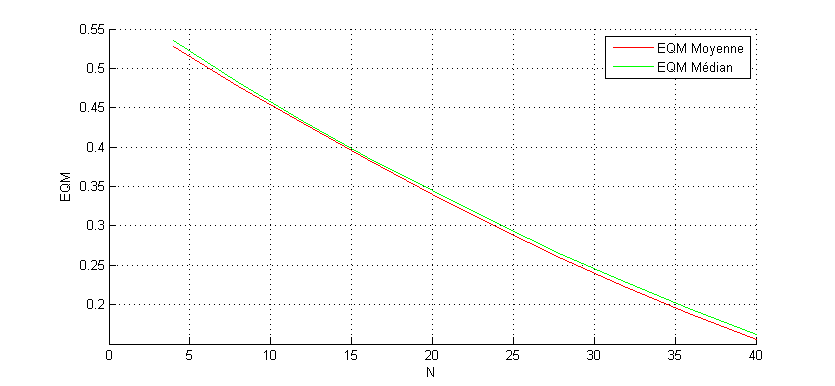
L’EQM est une mesure statistique qui permet de mesurer la différence entre deux vecteurs. La figure ci-dessous illustre l’erreur quadratique moyenne en fonction de la taille du filtre. On constate que l’erreur décroit avec l’augmentation de la taille du filtre, donc la qualité du signal s’améliore avec l’utilisation d’un filtre de taille importante. L’inconvénient majeur du filtre, il introduit un retard de N Echantillons 🙁
Programme Matlab
% Paramètres du signal
F0=10;
T0=1/F0;
Ns=200;
Fs=F0*Ns;
Ts=1/Fs;
% Génération du signal
t= 0:Ts:2*T0;
s_t= sin(2*pi*F0*t);
% Géneration du bruit
Vare = 1e-2;
Mu=0;
b_t = Mu + sqrt(Vare)*randn(1,length(s_t));
% Génération signal + bruit
s_b_t = s_t + b_t;
% Affichage
figure(1);
grid on ; hold on ;
plot(t, s_t,'r');
plot(t,b_t,'g');
plot(t,s_b_t,'b');
legend('Signal original', 'Bruit', 'Signal bruité');
xlabel('t(s)');
ylabel('s(t)');
%% Filtrage - Lissage du signal
% Paramètre du filtre moyenneur
N_filtre = 4:4:40 ;
S_filre = ones(length(N_filtre),length(s_t));
MSE=0*N_filtre;
for k=1:length(N_filtre)
S_filre(k,:) = s_t;
for i=N_filtre(k) : length(s_t)
S_filre(k,i) =mean( s_b_t(i-N_filtre(k)+1:i));
end
% Calcul de l'erreur quadratique moyenne
N_k= N_filtre(end);
D = abs( s_b_t(1:end-N_k+1) - S_filre(k,N_k:end)).^2;
MSE(k) = sum(D(:))/length(s_t);
end
% Affichage
figure(2);
grid on ; hold on ;
plot(t,s_t,'r');
plot(t,s_b_t,'b');
plot(t,S_filre,'g');
legend('Signal original','Signal bruité', 'Signal bruité filtré');
xlabel('t(s)');
ylabel('s(t)');
figure(3);
grid on ; hold on ;
plot(N_filtre,MSE,'r');
legend('EQM en fonction de N');
xlabel('N');
ylabel('EQM');Etude et simulation numérique du filtre Médian avec Matlab
Le filtre médian est un filtre numérique simple, souvent utilisé pour la réduction de bruit. La réduction de bruit est une étape de post-traitement classique visant à améliorer les résultats de traitements futurs du signal. La technique de filtre médian est largement utilisée en traitement d’images numériques et traitement des signaux en général car il permet sous certaines conditions de réduire le bruit dans le signal.
Le principe du filtre est très simple ! Il consiste à trié un morceau de N échantillons du signal (par ordre croissant ou décroissant), puis sélectionner la valeur médiane du tableau, c.à.d. la valeur de l’indice N/2 ! Alors la valeur médiane est égale à TabSort[N/2].

Résultats des simulations avec Matlab
Bruit filtré pour N varié de 4 à 40 avec un pas de 4
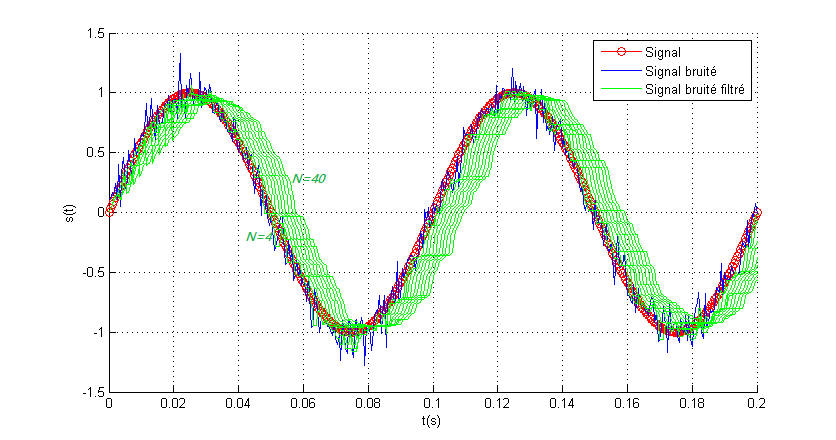
Bruit filtré pour N=40 & N=4
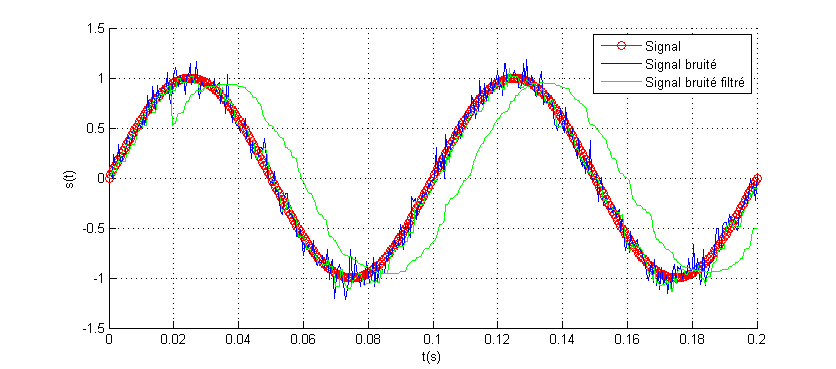
On constate que le filtre médian permet d’obtenir des bons résultats. On voit clairement que la qualité du signal filtré est dégradée par rapport au filtre moyenneur. La figure ci-dessous illustre la comparaison entre les EQM des deux filtres.
Programme Matlab
% Paramètres du signal
F0=10;
T0=1/F0;
Ns=200;
Fs=F0*Ns;
Ts=1/Fs;
% Génération du signal
t= 0:Ts:2*T0;
s_t= sin(2*pi*F0*t);
% Géneration du bruit
Vare = 1e-2;
Mu=0;
b_t = Mu + sqrt(Vare)*randn(1,length(s_t));
% Génération signal + bruit
s_b_t = s_t + b_t;
% Paramètres du filtre Médian
N_filtre = 4:4:40 ;
S_filre = ones(length(N_filtre),length(s_t));
MSE2=0*N_filtre;
for k=1:length(N_filtre)
S_filre(k,:) = s_t;
for i=N_filtre(k) : length(s_t)
MedTab= sort(s_b_t(i-N_filtre(k)+1:i));
S_filre(k,i) =MedTab(round(N_filtre(k)/2.0));
end
% Calcul de l'erreur quadratique moyenne
N_k= N_filtre(end);
D = abs( s_b_t(1:end-N_k+1) - S_filre(k,N_k:end)).^2;
MSE2(k) = sum(D(:))/length(s_t);
end
% Affichage
figure(1);
grid on ; hold on ;
plot(t,s_t,'r-o');
plot(t,s_b_t,'b');
plot(t,S_filre,'g');
legend('Signal','Signal bruité', 'Signal bruité filtré');
xlabel('t(s)');
ylabel('s(t)');
figure(2);
grid on ; hold on ;
plot(N_filtre,MSE2,'g');
legend('EQM en fonction de N');
xlabel('N');
ylabel('EQM');************

Une réponse sur « Projet électronique : Traitement du signal avec Arduino # Lissage & Seuillage d’un signal 1/3 »
[…] Etude et simulation numérique du filtre Moyenneur avec Matlab [1/3] […]