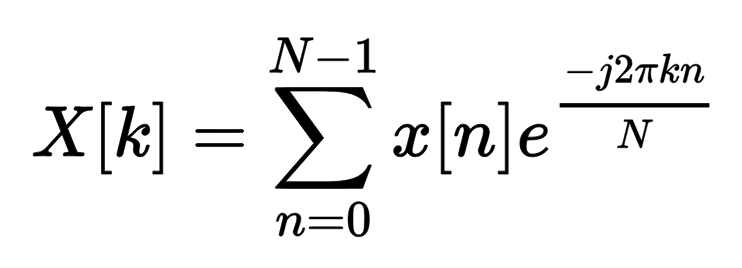Objectifs
- Savoir implémenter la DFT avec Matlab
- Savoir exploiter le spectre d’un signal avec Matlab
- Savoir extraire les amplitudes de la DFT
- Comprendre la notion de la fréquence
- Savoir la relation entre la fréquence et la longueur d’onde
- Savoir définir la fréquence d’échantillonnage
- Savoir la formule de la transformée de Fourier discrète (DFT)
- Comprendre la notion du spectre
- Etc.
Voir le tuto pour plus de détails
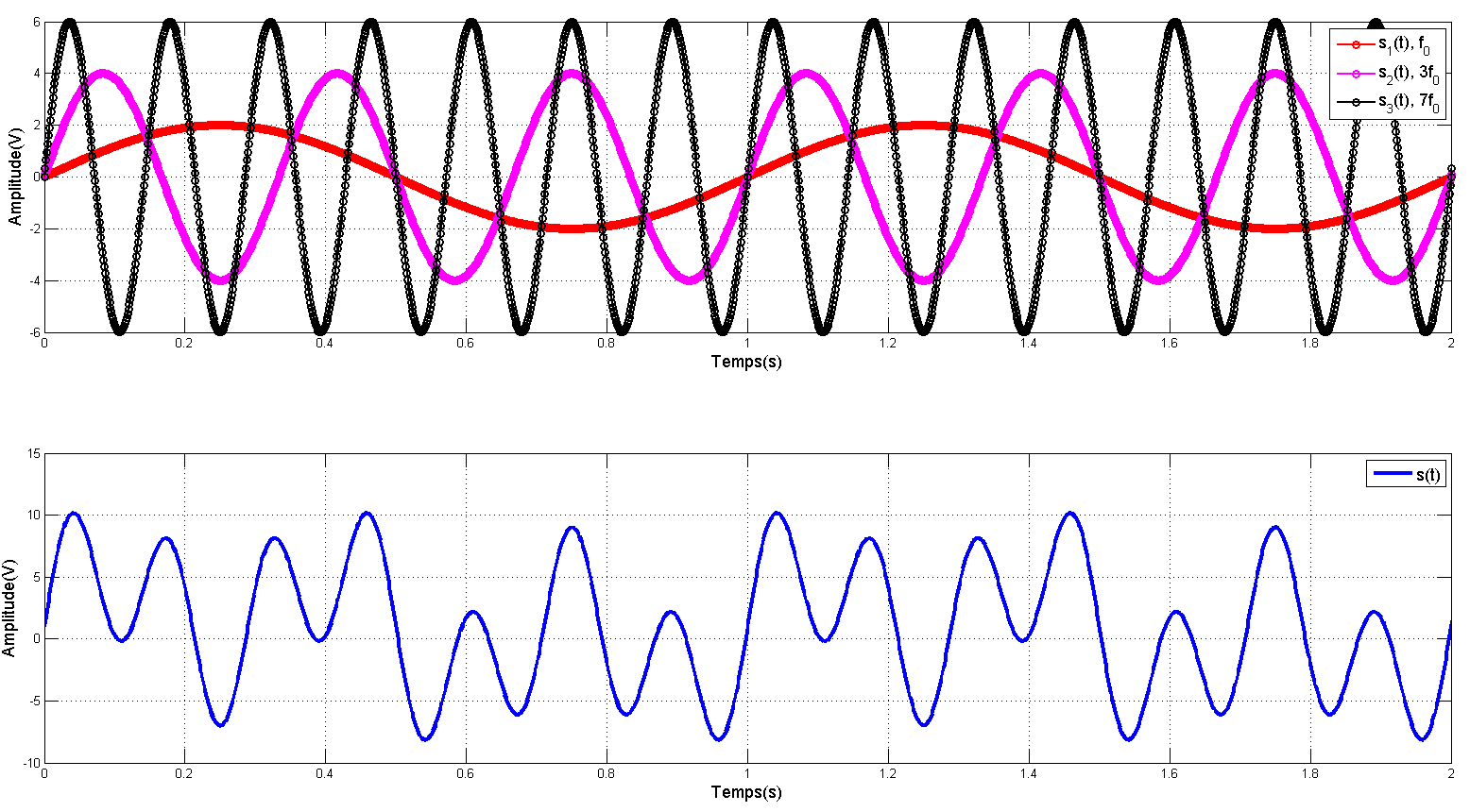
Analyse temporelle du signal (Code Matlab)
L’implémentation de la DFT (Digital Fourier Transform) consiste à implémenter l’équation ci-dessous.
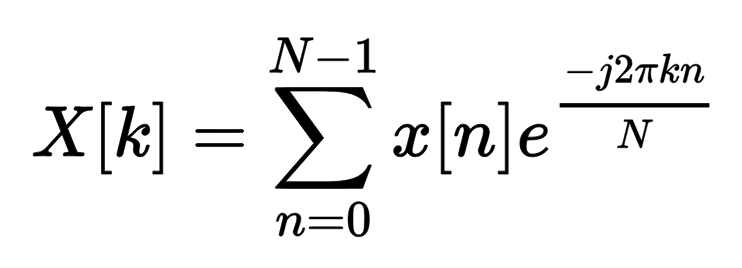
%% Signal temporel
N=2^12;
f0=1;t0=1/f0;
t=linspace(0,5*t0,N);
ts=t(2)-t(1); fs=1/ts;
s_0=1; % DC
s_1=2*sin(2*pi*f0*t); % f0
s_2=4*sin(2*pi*3*f0*t); % 3f0
s_3=6*sin(2*pi*7*f0*t); % 7f0
s_b=0*randn(1,N); % Bruit/Normal
s_t=s_0+s_1+s_2+s_3+s_b; % Signal
% Affichage
figure(1);
subplot(211);
plot(t,s_1,'r-o','LineWidth',2); hold on; grid on;
plot(t,s_2,'m-o','LineWidth',2);
plot(t,s_3,'k-o','LineWidth',2);
xlabel('Temps(s)','fontsize',13);
xlim([0 2*t0]);
ylabel('Amplitude(V)','fontsize',13);
legend({'s_1(t), f_0','s_2(t), 3f_0','s_3(t), 7f_0'},'fontsize',13);
set(gca,'color','none');
subplot(212);
plot(t,s_t,'b','LineWidth',3); hold on; grid on;
xlabel('Temps(s)','fontsize',13);
xlim([0 2*t0]);
ylabel('Amplitude(V)','fontsize',13);
legend({'s(t)'},'fontsize',13);
set(gca,'color','none');
Analyse fréquentielle d’un signal (Code Matlab)
%% Init
clear all;
close all;
clc;
%% Signal temporel
N=2^12;
f0=1;t0=1/f0;
t=linspace(0,5*t0,N);
ts=t(2)-t(1); fs=1/ts;
s_0=1; % DC
s_1=2*sin(2*pi*f0*t); % f0
s_2=4*sin(2*pi*3*f0*t); % 3f0
s_3=6*sin(2*pi*7*f0*t); % 7f0
s_b=0*randn(1,N); % Bruit/Normal
s_t=s_0+s_1+s_2+s_3+s_b; % Signal
% Affichage
figure(1);
subplot(211);
plot(t,s_1,'r-o','LineWidth',2); hold on; grid on;
plot(t,s_2,'m-o','LineWidth',2);
plot(t,s_3,'k-o','LineWidth',2);
xlabel('Temps(s)','fontsize',13);
xlim([0 2*t0]);
ylabel('Amplitude(V)','fontsize',13);
legend({'s_1(t), f_0','s_2(t), 3f_0','s_3(t), 7f_0'},'fontsize',13);
set(gca,'color','none');
subplot(212);
plot(t,s_t,'b','LineWidth',3); hold on; grid on;
xlabel('Temps(s)','fontsize',13);
xlim([0 2*t0]);
ylabel('Amplitude(V)','fontsize',13);
legend({'s(t)'},'fontsize',13);
set(gca,'color','none');
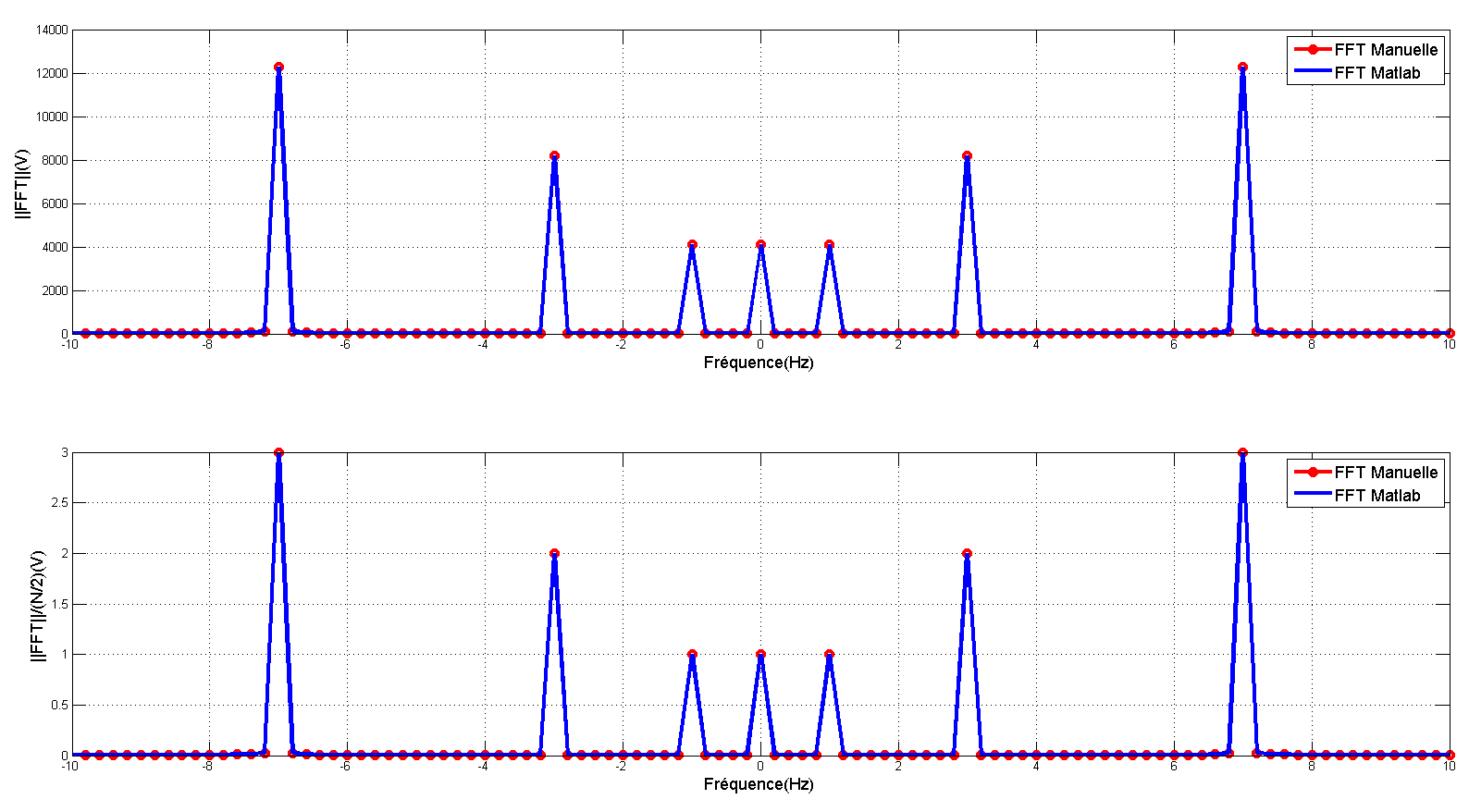
%% Spectre fréquentiel
% Calcul de la DFT (Manuelle)
nfft=floor(N);
df=fs/nfft;
f=linspace(-fs/2-df,fs/2,nfft);%
s_f=zeros(1,nfft);
for k=0:nfft-1
somme=0.0;
for j=0:N-1
somme=somme+(s_t(j+1)*exp(-1i*2*pi*k*j/N));
end
s_f(k+1)= somme;
end
% Calcul de la DFT (Matlab)
s_fm=fft(s_t,nfft);
% Affichage
figure(2);
subplot(211);
plot(f,fftshift(abs(s_f)),'r-o','LineWidth',3); hold on; grid on;
plot(f,fftshift(abs(s_fm)),'b-','LineWidth',3);
xlabel('Fréquence(Hz)','fontsize',13);
% xlim([f(1) f(end)]);
xlim([-10*f0, 10*f0]);
ylabel('||FFT||(V)','fontsize',13);
legend({'FFT Manuelle','FFT Matlab'},'fontsize',13);
set(gca,'color','none');
subplot(212);
plot(f,fftshift((abs(s_f))/(N)),'r-o','LineWidth',3); hold on; grid on;
plot(f,fftshift((abs(s_fm))/(N)),'b-','LineWidth',3);
xlabel('Fréquence(Hz)','fontsize',13);
% xlim([f(1) f(end)]);
xlim([-10*f0, 10*f0]);
ylabel('||FFT||/(N/2)(V)','fontsize',13);
legend({'FFT Manuelle','FFT Matlab'},'fontsize',13);
set(gca,'color','none');
On verra dans le prochain tuto l’implémentation en C sur Arduino et le test de la DFT.