Définition 

ASCII signifie American Standard Code for Information Interchange. Il dispose de 128 codes ASCII standards, chacun d’entre eux peut être représenté par un nombre binaire codé sur 7 bits ayant des valeurs comprises entre 0000000 (0) et 1111111 (127). E code ASCII est étendu de 128 caractères supplémentaires qui font en total 256 caractères (8 bits), qui varient selon les ordinateurs, les programmes et les polices.

Code ASCII 

  Dec Hex Code	 Dec Hex Code	 Dec Hex Code	 Dec Hex Code
   0  00  ^@	  32  20    	 64  40   @	  96  60   `
   1  01  ^A	  33  21   !	 65  41   A	  97  61   a
   2  02  ^B	  34  22   "	 66  42   B	  98  62   b
   3  03  ^C	  35  23   #	 67  43   C	  99  63   c
   4  04  ^D	  36  24   $	 68  44   D	 100  64   d
   5  05  ^E	  37  25   %	 69  45   E	 101  65   e
   6  06  ^F	  38  26   &	 70  46   F	 102  66   f
   7  07  ^G	  39  27   '	 71  47   G	 103  67   g
   8  08  ^H	  40  28   (	 72  48   H	 104  68   h
   9  09  ^I	  41  29   )	 73  49   I	 105  69   i
  10  0A  ^J	  42  2A   *	 74  4A   J	 106  6A   j
  11  0B  ^K	  43  2B   +	 75  4B   K	 107  6B   k
  12  0C  ^L	  44  2C   ,	 76  4C   L	 108  6C   l
  13  0D  ^M	  45  2D   -	 77  4D   M	 109  6D   m
  14  0E  ^N	  46  2E   .	 78  4E   N	 110  6E   n
  15  0F  ^O	  47  2F   /	 79  4F   O	 111  6F   o
  16  10  ^P	  48  30   0	 80  50   P	 112  70   p
  17  11  ^Q	  49  31   1	 81  51   Q	 113  71   q
  18  12  ^R	  50  32   2	 82  52   R	 114  72   r
  19  13  ^S	  51  33   3	 83  53   S	 115  73   s
  20  14  ^T	  52  34   4	 84  54   T	 116  74   t
  21  15  ^U	  53  35   5	 85  55   U	 117  75   u
  22  16  ^V	  54  36   6	 86  56   V	 118  76   v
  23  17  ^W	  55  37   7	 87  57   W	 119  77   w
  24  18  ^X	  56  38   8	 88  58   X	 120  78   x
  25  19  ^Y	  57  39   9	 89  59   Y	 121  79   y
  26  1A  ^Z	  58  3A   :	 90  5A   Z	 122  7A   z
  27  1B  ^[	  59  3B   ;	 91  5B   [	 123  7B   {
  28  1C  ^\	  60  3C   <	 92  5C   \	 124  7C   |
  29  1D  ^]	  61  3D   =	 93  5D   ]	 125  7D   }
  30  1E  ^^	  62  3E   >	 94  5E   ^	 126  7E   ~
  31  1F  ^_	  63  3F   ?	 95  5F   _	 127  7F   

Avant d’introduire la notion de compression, nous allons survoler quelques codes relativement courants. La définition d’un code est un symbole remplaçant un autre. Dans la cadre informatique, il s’agira d’une suite binaire qui remplacera un symbole donné (souvent un caractère).

Codage et Compression de données

Les tables de caractères

ASCII

Le code ASCII (American Standard Code for Information Interchange) est un code de 7 bits (de données) et d’un bit de parité par symbole. Il date de 1961, et fut créé par Bob Bemer. 128 (= [latex]2^7[/latex]) symboles peuvent donc être codés. On y retrouve les lettres majuscules et minuscules, les 10 chiffres, quelques symboles de ponctuation et des caractères de contrôle.

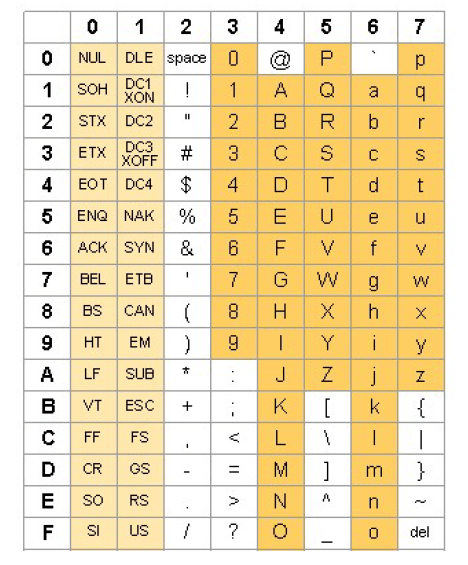
On entend régulièrement parler du code ASCII étendu (extended ASCII). Ce code n’est en réalité pas clairement déterminé, en ce sens qu’il n’est pas unique, plusieurs variantes non compatibles ayant été publiées. Les plus courants sont le code ASCII étendu OEM, et le code ASCII étendu ANSI. L’objectif principal était de permettre l’utilisation des caractères accentués, absents de la table ASCII basique. Chaque caractère y est représenté par une chaine de 8 bits.

EBCDIC

Il s’agit d’un mode de codage des caractères sur 8 bits créé par IBM à l’époque des cartes perforées. De nombreuses versions existent, bien souvent incompatibles entre elles, ce qui est en partie la cause de son abandon. On l’utilise encore de nos jours, mais presque essentiellement pour des raisons de rétrocompatibilité.

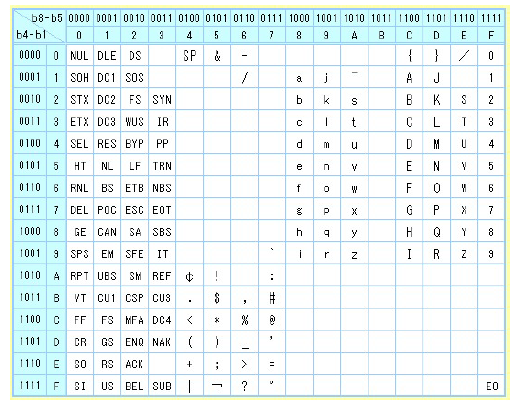
ISO 8859-1 (et -15)

C’est une norme de l’International Organization for Standardization, souvent dénommée Latin-1. Elle se compose de 191 caractères codés sur un octet. Cette norme recouvre les caractères plus utilisés dans les langues européennes et dans une partie des langues africaines.

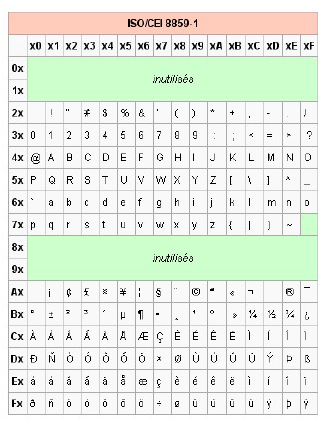
Comme on le voit sur la figure 1.5, certaines plages ne sont pas utilisées : les codes 0x00 à 0x1F et 0x7F à 0x9F ne sont pas attribuées. Pour permettre l’utilisation du sigle €, il a fallu mettre cette table à jour. La norme ISO 8859-15 est alors apparue. Elle se compose des mêmes éléments que la norme ISO 8859-1, mis à part 8 caractères, illustrés à la figure 1.6.

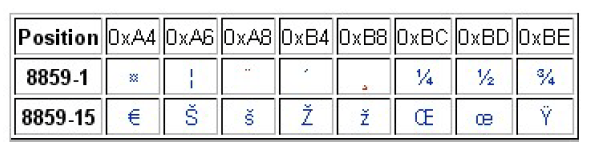
Unicode

Ce projet fut initié en 1987 par Becker, Collins et Davis. L’objectif était alors de construire un code universel sur 16 bits, permettant donc 65,536 (216) codes différents. En 1991 est fondé le consortium Unicode, comprenant des linguistes et autres spécialistes de nombreux horizons. La norme Unicode est, en plus d’un standard de codage de caractères, un immense rapport des recherches mondiales sur les langues utilisées et ayant été utilisées à travers le monde.

Unicode en est actuellement à la version 5.0, le nombre de caractères identifiés étant sans cesse croissant. La version 3.0 (1999) comptait déjà 49.194 caractères, la limite des 216 étant déjà bien proche. En 2001, la version 3.2 ajouta un peu moins de 45.000 caractères. L’espace des codes Unicode s’étend de 0 à 0x10FFFF. Un code sur 16 bits n’est donc plus suffisant. Le codage sur 4 octets permet la représentation de plus de 4 milliards de caractères (232). On y retrouve le code ASCII, auquel on a notamment ajouté les jeux complets de caractères coréens, japonais et chinois, mais aussi les symboles mathématiques ou encore les écritures anciennes telles que l’écriture cunéiforme ou le linéaire B.

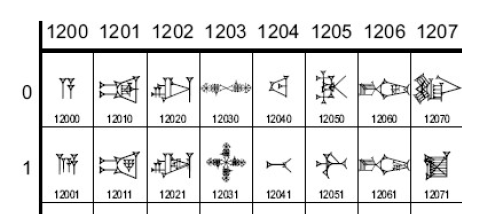
Plusieurs formats d’encodage sont possibles (UTF – Universal Transformation Format) :

• UTF-8 : 8 bits
• UTF-16 : 16 bits
• UTF-32 : 32 bits

Le standard Unicode définit les caractères comme une série de points de code (codepoints). Selon le format utilisé, sa représentation sera différente.

UTF-8

Les codepoints encodés sous ce format se présentent comme un octet ou une suite d’octets. Lorsque le caractère se situe dans la plage 0x00 à 0x7F, il s’agit du code ASCII, ce qui ne pose pas de problème pour le représenter sur un seul octet. Pour les autres valeurs, un premier octet (lead byte) suivi d’un nombre variable d’octets (trailing byte)(maximum 4 octets au total) représentent conjointement la valeur à encoder. Dans le cas où on utilise un lead byte, celui devra toujours avoir son bit de poids fort à 1, et sera suivi d’autant de bit à 1 que de trailing byte.

Les bits remplacés par ’-’ dans le tableau ci-dessus représente les bits disponibles pour la valeur Unicode à encoder. Toutefois, chaque trailing byte doit avoir ses deux premiers bits à 10. Ainsi, chaque trailing byte possédera 6 bits d’information.

La limite de 21 bits est suffisante pour représenter l’ensemble des codepoints définis par Unicode. Par cette méthode d’encodage, un même caractère peut avoir plusieurs représentations. Par exemple, le caractère ’/’ peut s’écrire

• 0x2F
• 0xC0 0xAF
• 0xE0 0x80 0xAF
• 0xF0 0x80 0x80 0xAF

Depuis la troisième version d’Unicode, il a été spécifié que seul l’encodage le plus court était accepté.

UTF-16

Les codepoints sont ici exprimés sous la forme de mots de 16 bits. La plupart des caractères courants sont représentables sur 16 bits, mais certains ne le sont toutefois pas (la plage adressable Unicode étant étendue jusque 0x10FFFF). Similairement à l’UTF-8, il est possible d’utiliser plusieurs mots (maximum 2) de 16 bits afin d’encoder des valeurs nécessitant plus de 16 bits. Afin de déterminer les mots de 16 bits, on a recours au calcul suivant (U représente la valeur Unicode) :

• Si U < 0x10000, U est encodé comme un entier non signé sur 16 bits.
• Soit U’ = U – 0x10000. U étant inférieur ou égal à 0x10FFFF (par définition de la plage de validité du standard Unicode), U’ sera inférieur ou égal à 0xFFFFF. 20 bits sont donc nécessaires.
• Initialiser 2 entiers non signés de 16 bits, W1 et W2, aux valeurs 0xD800 et 0xDC00.
• Chaque entier possédera 10 bits libres, qui fourniront au total les 20 bits nécessaires.
• Associer les 10 bits de poids forts de U’ aux bits libres de W1, et les 10 autres bits de U’ (les 10 bits de poids faibles de U’) à W2. Il n’y ici qu’une seule manière de représenter un codepoint donné.

UTF-32

Les codepoints sont ici représentés par une valeur sur 32 bits. Cette taille est suffisante pour représenter tous les codepoints Unicode existants.

Base64

Largement utilisé pour la transmission de messages, le codage Base64 utilise, comme son nom le laisse présager, un alphabet de 64 caractères. Un 65ème caractère existe, mais ne fait pas partie de l’alphabet à proprement parlé. Il est utilisé comme caractère final (’=’).

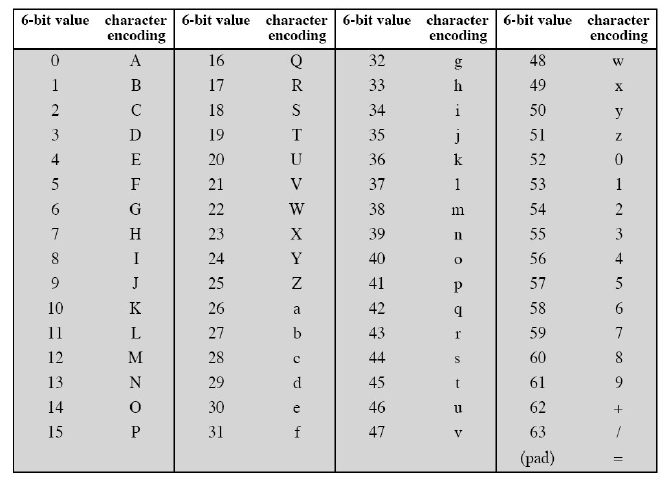
Le traitement s’opère par groupe de 24 bits (3 octets) et produit en sortie un bloc de 4 caractères (4*6 bits). Chaque groupe de 6 bits sert d’index dans l’alphabet Base64, et le caractère associé sera placé sur le flux de sortie. Lorsque le nombre de bits en entrée devient insuffisant (le flux d’entrée est composé de moins de 24 bits), seules deux possibilités existent (en sachant que l’entrée ne peut être constituée que
d’octets entiers) :

• l’entrée fournit 8 bits (1 octet) : le bloc de 4 caractères en sortie sera composé de 2 caractères de la table base64 suivis de 2 caractères finaux (c’est-à-dire le 65ème caractère).
• l’entrée fournit 16 bits (2 octets) : le bloc de 4 caractères en sortie sera composé de 3 caractères de la table base64 suivis de 1 caractère final.

Exemple Le mot “oui” est traduit sous forme binaire en ’01101111 01110101 01101001’. Si on découpe ces 24 bits en blocs de 6 bits, il vient ’011011 110111 010101 101001’. Sous forme décimale, on obtient ’27 55 21 41’, et en substituant, il vient ’b3Vp’.

Lorsqu’on utilise cet encodage dans le logiciel de chiffrement de messages PGP, le résultat est ensuite encodé au format ASCII. Retour à l’exemple Ainsi, si on met le bit de parité à 0, la correspondance de ’b3Vp’ est ’01100010 00110011 01010110 01110000’.

La compression de données

La compression a pour but de réduire la longueur d’une chaîne sans affecter son contenu informatif. Cela permet à la fois de réduire les exigences en mémoire et d’augmenter la capacité d’un canal de transmission (théorie de Shannon). L’information d’un message peut se définir comme la « surprise » causée par la connaissance de ce message. Elle se calcule par la formule

[latex] -log_2 p[/latex]

si p est la probabilité d’occurrence du message. Soit l’ensemble X composé de N messages dont les probabilités d’occurrence sont données
par [latex]p_1[/latex], …, [latex]p_N[/latex]. Alors:

[latex] \sum_{i=1,\ i\neq j}^N p_{i}=1[/latex]

L’information H associée à ces N messages est définie comme la « surprise moyenne » :

[latex] -\sum_{i=1,\ i\neq j}^N -log_2 p[/latex]

H(x) permet de mesurer l’information. On lui donne le nom d’Entropie.

0 < H < inf

et est maximale quand [latex]p_1=p_1=…=p_N=\frac{1}{N}[/latex]

Indépendance des messages

Soit un ensemble C de messages égal au produit de 2 ensembles A et B indépendants. Alors

H(C) = H(A) + H(B)

En effet,

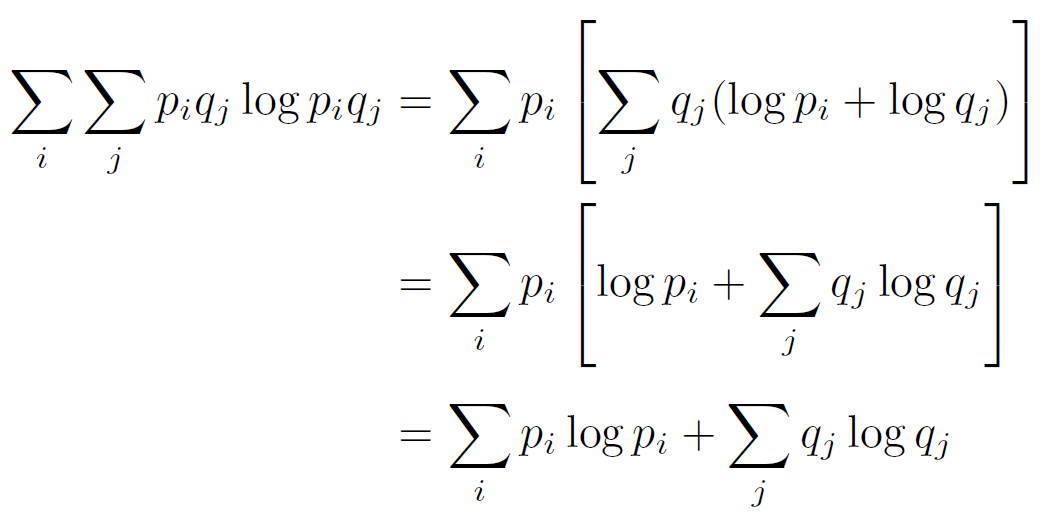
Longueur moyenne d’un code

Soit un codage des messages à partir d’un alphabet de d caractères tel qu’il existe une correspondance non ambiguë entre chaque message et son code. Si le message i est représenté par une séquence de li caractères, la longueur moyenne d’un code est donnée par la formule suivante :

[latex]<L> =\sum_{i=1,\ i\neq j}^N p_{i}l_i[/latex]

Algorithme du codage de Huffman

1. Les messages constituent les feuilles d’un arbre portant chacune un poids égal à la probabilité P d’occurrence du message correspondant
2. Joindre les 2 noeuds de moindre poids en un noeud parent auquel on attache un poids égal à la somme de ces 2 poids
3. Répéter le point 2 jusqu’à l’obtention d’une seule racine à l’arbre (de poids [latex] \sum_{i=1,\ i\neq j}^N p_{i}=1[/latex])
4. Affecter les codes 0 et 1 aux noeuds descendants directs de la racine
5. Continuer à descendre en affectant des codes à tous les noeuds, chaque paire de descendants recevant les codes L0 et L1 où L désigne le code associé au parent.

Par exemple, soit un ensemble de 3 messages a, b et c de probabilité respective 0.6, 0.3 et 0.1. La construction de l’algorithme est donnée à la figure 1.10.

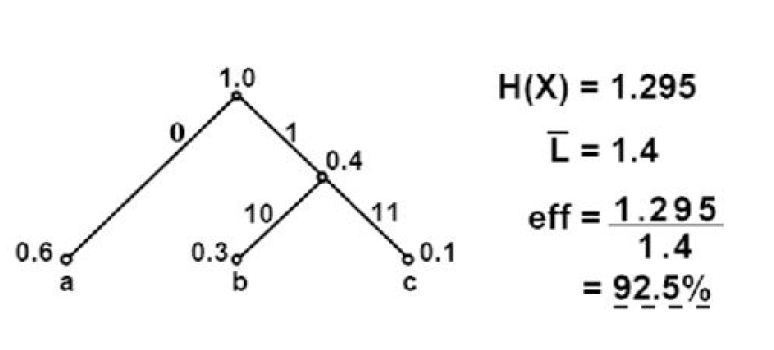
En codant des séquences de plus en plus longues, l’efficacité tend vers 100% (mais le gain est de moins en moins important, comme on le voit sur la figure).

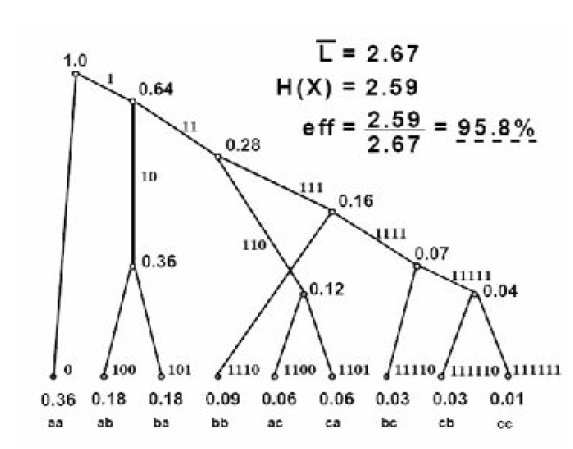
En résumé, l’algorithme de HUFFMAN donne un codage optimal (car la redondance est minimale) et possède la propriété préfixe (ce qui est intéresssant en cas de transmission sur un canal).

Codage de Shannon-Fano

Ce procédé est antérieur au codage de Huffman est se base également sur un codage statistique.

Algorithme

1. Construire une table des fréquences d’apparition des symboles triée par ordre décroissant.
2. Diviser cette table en deux parties. Celles-ci doivent avoir une somme de fréquences égale (ou pratiquement égale) à celle de l’autre.
3. Affecter le chiffre binaire 0 à la moitié inférieure, la moitié supérieure prenant la valeur 1.
4. Répéter les opérations 2 et 3 aux deux parties, jusqu’à ce que chaque symbole ne représente plus qu’une partie de la table.

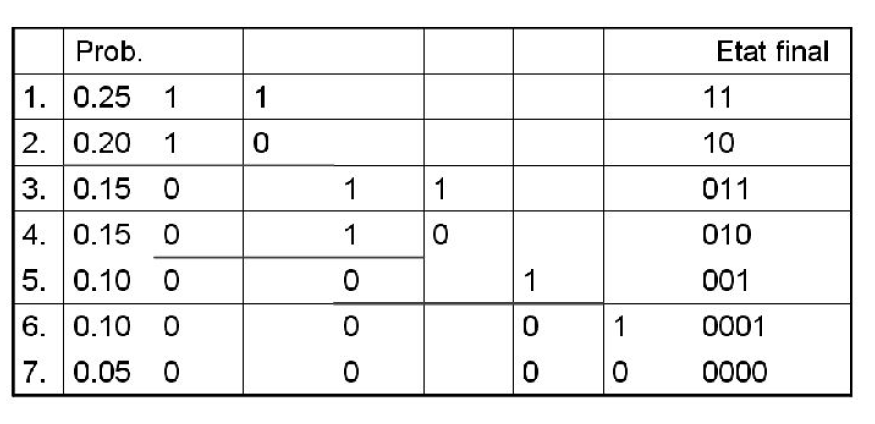
Le codage de HUFFMAN est efficace quand il y a un petit nombre de types de messages dont quelques-uns couvrent une proportion importante du texte ([latex]p_i >> p_j)[/latex]. Quand le nombre de types de messages augmente et que les fréquences sont plus uniformes ([latex]p_i \simeq p_j[/latex] ), le gain est négligeable.

Souvent, le nombre de messages différents est indéterminé à l’avance (par exemple quand il s’agit de mots dans un texte simple) ou trop grand pour justifier un codage à longueur variable (par exemple, le jeu de caractères ASCII). Dans ces cas, on effectue une compression en remplaçant seulement des séquences choisies de texte par des codes plus courts. Il y a plusieurs façons de procéder :

• parcourir le texte et remplacer les séquences redondantes par des séquences plus courtes (RLE)
• analyser préalablement le texte pour déterminer les groupes à remplacer et les codes qui les remplacent (LZW)
• …

Codage RLE (Variantes)

Le codage RLE (Run-Length Encoding) est, comme son nom l’indique, un codage de « course », c’est-à-dire qu’il élimine certaines séquences de caractères en les remplaçant par un code spécifique. Chaque « course » de k éléments (2 < k _ 9) est remplacée par un caractère non utilisé (ex : @) suivi de l’entier k et du caractère substitué.

Exemple 1 « AB200003944445260D666@A2 » est remplacé par « AB2@40394@445260D@36@@A2 ».

Si tous les caractères sont utilisés, on en choisit un rarement utilisé comme « indicateur » et on le double quand on rencontre ce caractère rare. Ce principe est illustré dans l’exemple ci-dessus. On remarque également que dans le cas précis où on se met d’accord pour ne remplacer que les courses d’un caractère donné, il n’est pas nécessaire de fournir le caractère remplacé. Ce type d’utilisation est fréquent dans le cas des transmissions d’image en noir et blanc (type fax).

Exemple 2 « AB20000394000005260D000A2 » est remplacé par « AB2@4394@55260D@3A2 ».

Une condition est nécessaire pour que cette compression soit utile : la séquence répétée doit contenir au moins 4 éléments pour obtenir un gain (3, dans le cas où on est d’accord sur le caractère remplacé).

Utilisation d’une bit-map

Il est facile de laisser tomber des champs entiers d’un enregistrement. Prenons un enregistrement de 4 champs de 8 caractères (32 caractères) pour les noms alors que la longueur moyenne est bien plus courte. On utilise alors la technique du bit-mapping. Le principe est d’utiliser une bit-map devant chaque enregistrement pour indiquer la présence ou l’absence de valeur dans les différents champs.

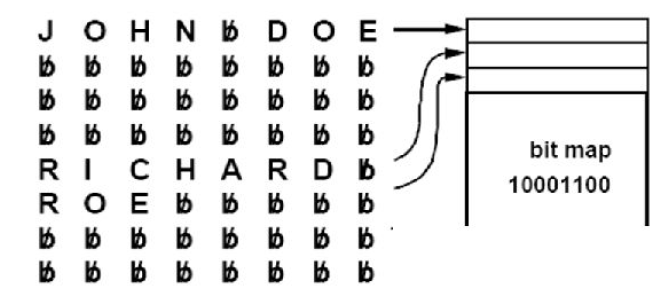
Recherche de pattern

Par une étude sur des textes anglais, on a pu déterminer que le nombre de mots distincts utilisés représentait 10 à 15% du nombre total de mots dans le texte. Ce pourcentage est encore plus petit pour les textes liés à des domaines spécialisés (articles scientifiques, documents militaires, médicaux, …). Dès lors, on pourrait remplacer des mots ou «patterns» préalablement choisis.

Cependant, le gain est limité par 2 observations :

• les mots les plus courants sont courts (the, a, to, in, …),
• par loi de ZIPF : la fréquence du nieme mot le plus courant est proportionnelle à 1/n, c’est-à-dire que le gain augmente de plus en plus lentement quand on code de plus en plus de mots.

Il existe tout de même quelques pistes de solution :

• on peut coder des « digrammes », c’est-à-dire remplacer des paires de lettres par un seul caractère. Ainsi, on pourrait remplacer les paires « ES », « TR », « LL »,… par un caractère propre. On obtient dans ce cas une compression d’environ 50% en moyenne.
• on peut aussi coder les « patterns » les plus courants : cette technique s’utilise lorsque des mots apparaissent fréquemment (ex : vocabulaire informatique) mais

1. l’analyse préalable pour les déterminer est coûteuse :

• il faut tenir compte d’un nombre élevé de candidats, et
• le choix d’un pattern peut affecter l’utilité des précédents. Par exemple, si la séquence ’ere’ est choisie puis également ’here’, ’there’ et ’where’, si on commence par remplacer les séquences les plus longues, le codage de ’ere’ devient beaucoup moins utile.

2. cela peut gêner la recherche :

• Par exemple, si ’ing l’ est codé par ’#’ et ’ing t’ par ’@’, et si ’string’ est codé par ’str#’ dans le contexte ’string lists’ et par ’str@’ dans le contexte ’string trees’. La recherche de ’string’ conduit à analyser plus d’un pattern.

La compression par antidictionnaire

Un antidictionnaire est un ensemble de mots qui n’apparaissent pas dans le texte. Pour mieux comprendre son fonctionnement, nous allons l’illustrer par un exemple :

• Soit un texte (binaire) que l’on souhaite compresser.
• Imaginons que le mot ’1001’ soit dans l’anti-dictionnaire.
• Dès lors, on pourra coder la séquence ’1000’ par ’100’.
• En effet, sachant que le mot ’1001’ est dans l’anti-dictionnaire, c’est donc que ce même mot n’est pas dans le texte à coder. Donc seul un ’0’ peut suivre la séquence ’100’ dans le texte.

Catégorisation des compressions

Il existe plusieurs manières de classer les formats de compression. On peut notamment les scinder comme suit :

• Par analyse statistique ou par dictionnaire : Huffman VS LZW
• Avec ou sans perte (= destructive ou non destructive) :
  • Avec perte : des détails sont détruits lors de la compression, et il est impossible de les retrouver par la suite. On utilise les propriétés de l’oreille et de l’oeil humain pour supprimer les informations inutiles. Exemple : Jpeg
  • Sans perte : aucune perte et restitution parfaite après décompression. Exemples : Huffman, RLE, Zip, …
• Symétrique ou asymétrique :
  • Symétrique : le temps de calcul nécessaire pour la compression ou la décompression est équivalent. Il s’agit par exemple d’algorithmes de transmission de données.
  • Asymétrique : l’une des deux phases est plus rapide que l’autre, tels que les algorithmes d’archivage massif.

Ressources

Ressources bibliographiques : Data compression, the complete reference, David Salomon, 2004, Springer. Introduction to Data compression, Khalid Sayood, 2006, Morgan Kaufmann.

 

Illustrations :

• Data Compression, the complete reference, David Salomon, 2004, Springer
• Computer and Network Security, 3rd edition, W. Stallings, 2003, Prentice Hall
• Wikipedia.org

Le stockage des données

Après codage des informations, les données doivent être stockées sur un support quelconque. Dans la suite du cours, nous expliciterons :

• les supports de type carte magnétique
• les supports optiques
• CD (laser infrarouge – 780nm)
• DVD (laser rouge – 650nm)
• HD-DVD (laser bleu – 405nm)
• Blu-Ray (laser bleu – 405nm)
• les supports utilisant la technologie holographique

Représentation de quelques grandeurs binaires

Dans la figure , on compare des tailles en octets à des tailles plus « physiques ». L’erreur d’approximation est volontaire, dans un but de représentation.

Le support magnétique

Le principe est d’encoder les informations à partir d’un champ magnétique. La bande magnétique est constituée de pigments (p.ex. oxyde de fer). Par l’intermédiaire d’une tête d’écriture (un électro-aimant), on induit un champ magnétique qui va « marquer » ces pigments et ainsi y retenir une information. On parle de support « coercitif ».

Lors d’une lecture, la tête remarquera ces modifications de champs magnétiques. La tension électrique induite sera traduite et restituera les informations. Les supports magnétiques sont encore couramment utilisés : disquettes, bandes magnétiques et disquettes haute-densité (Zip, Jaz, SuperDisk, PeerLess,…). Ce support rencontre toutefois plusieurs problèmes :

• Usure relativement rapide
• Consommation forte en énergie
• Taille de certains supports de stockage

En raison de ces inconvénients, des recherches sont actuellement menées (notamment chez HP). Le type de stockage résultant porterait le nom de « Stockage à résolution atomique ».

Stockage à résolution atomique (ARS)

Ce type de support de stockage permettrait 1000 Gbits/in2 (1 inch = 2.54 cm). Le principe est d’utiliser un réseau de pointes microscopiques qui écrivent et lisent sur un matériau spécifique. Une partie mécanique déplacera le support d’écriture. Ce matériau a la particularité de posséder deux états selon sa température, l’un servant à l’écriture, l’autre à la lecture.

Une pointe sous tension envoie un faisceau d’électrons qui écrira sur le matériau lorsque la température sera assez élevée, et après refroidissement, une autre pointe lira sur la surface à l’aide d’un faisceau plus faible. Plusieurs problèmes importants restent à résoudre :

• Le mécanisme de déplacement doit avoir une précision de l’ordre du nanomètre
• Le système doit s’utiliser dans une atmosphère fermée pour éviter la dispersion des électrons à la sortie de la pointe

Support optique

En règle générale, pour les supports optiques, on utilisera le système de fichiers UDF (Universal Disk Format). Celui-ci est propre au stockage de données sur disque optique. Descendant de la norme ISO9660, c’est par son intermédiaire qu’il est possible d’ajouter des fichiers sur un disque après une première gravure (multi-session). Enfin, ce système de fichiers offre une compatibilité entre les systèmes d’exploitation (DOS, Windows, Linux, OS/2, Macintosh et UNIX)

CD-Rom :

Les données sont « incrustées » dans une couche de plastique (polycarbonate) et recouvertes par une couche d’aluminium (ou d’or, ou d’argent). Le tout est recouvert par une couche de vernis et par une couche utilisée pour la présentation du disque (label). Ce type de stockage est durable car aucune partie du lecteur ne touche la surface des données. Il utilise les propriétés de réfraction de la lumière pour identifier les 1 et les 0 d’après les creux et plats (pits and lands).

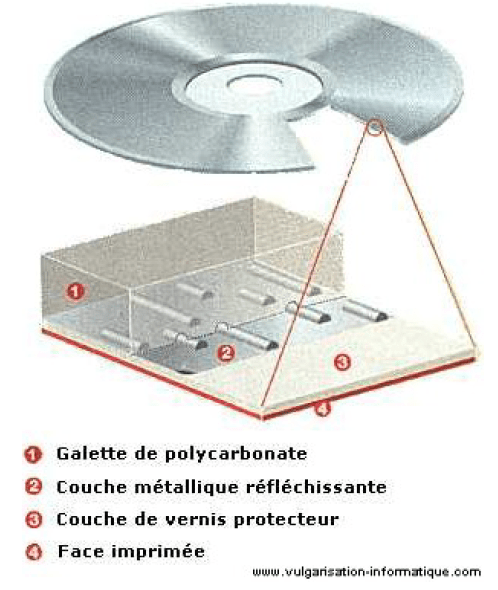
La structure logique d’un CD se compose de 3 parties :

• – La zone Lead-In : il s’agit de la zone la plus proche du centre du disque. Elle contient la TOC (Table of Content) permettant au lecteur de situer les données sur le disque.
• – La zone de données
• – La zone Lead-Out : elle contient des données nulles marquant la fin du disque. La technique d’Overburning permet d’écrire des données dans cette zone.

La capacité d’un disque audio varie de 74 à 99 minutes, de 650 à 870 MB. Ces tailles ont été au départ spécifié dans des normes : Yellow Book pour le CD-ROM, Red Book pour le cd audio, Orange Book pour les CD-R, Green Book pour les CD-i, etc. Sur un cd audio, chaque seconde occupe 75 secteurs du disque. Ainsi, un cd audio “plein” possède une capacité totale égale à 74x60x75 = 333.000 secteurs. La taille de ces secteurs dépend du contenu qu’ils renferment, un secteur de données audio nécessitant une correction d’erreurs moins importante (laissant donc place à plus d’information utile) que pour des données classiques (2353 octets contre 2048).

Un disque audio de 74 minutes possède donc une capacité de 783.216.000 octets (746MB) contre 681.984.000 octets (650MB) pour un CD de données. Des calculs semblables expliquent les différences en termes de capacité pour les disque de 80, 90 et 99 minutes.

CD-R

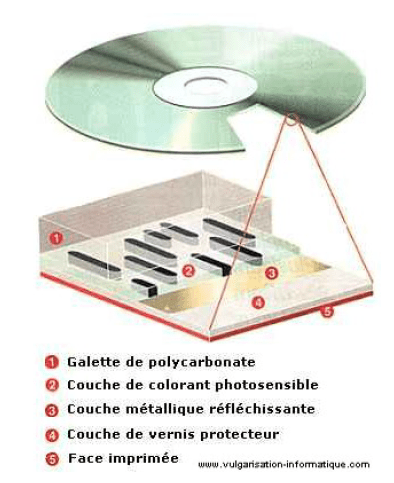
• Le laser utilisé pour bruler la couche photosensible est dix fois plus puissant que celui utilisé pour la lecture.
• La couleur du CD-R varie selon le colorant utilisé pour sa fabrication. Selon ce dernier, la réflexion sera plus ou moins bonne, ce qui influera sur sa qualité et sa durée de vie.
• On trouve une spirale pré-imprimée sur le CD-R. Elle est nécessaire pour guider le laser du graveur.
• Deux zones supplémentaires s’ajoutent aux trois déjà présente sur le CD-Rom. La PCA (Power Calibration Area) permet au graveur de calibrer la puissance du laser pour les phases d’écriture et de lecture.
• La PMA (Power Memory Area) retient la position des sessions écrites mais non finalisées
  (lorsqu’elles le sont, elles sont placées dans la zone de Lead-in).

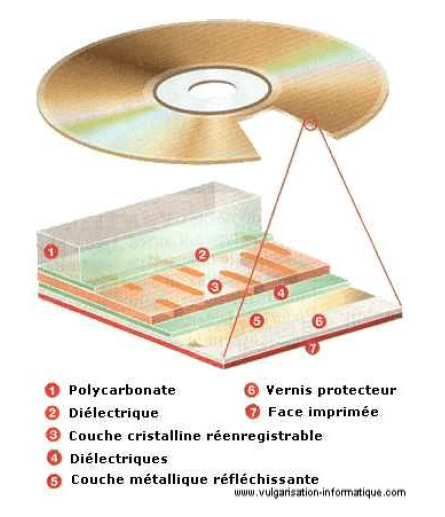
CD-RW

La couche inscriptible est un alliage de plusieurs matériaux (argent, indium, antimoine, et tellure). Deux couches diélectriques sont insérées entre le polycarbonate, cette couche inscriptible et la couche métallique réfléchissante. Suivant la température appliquée, diverses réactions ont lieu au niveau des atomes la composant, ayant pour effet de laisser passer ou non la lumière.

Le codage de l’information sur un CD

L’information codée sur un cd-rom utilise le codage EFM, Eight-to-Fourty Modulation, traduisant 8 bits en 14. La contrainte de ce codage est que deux bits à 1 ne peuvent être distants de moins de 2 bits à 0 et ne peuvent être séparés par plus de 10 bits à 0. On note cette contrainte (2,10). Le codage EFM fait partie de la famille des codes RLL (Run Lenght Limited), et on le note ici RLL(2,10).

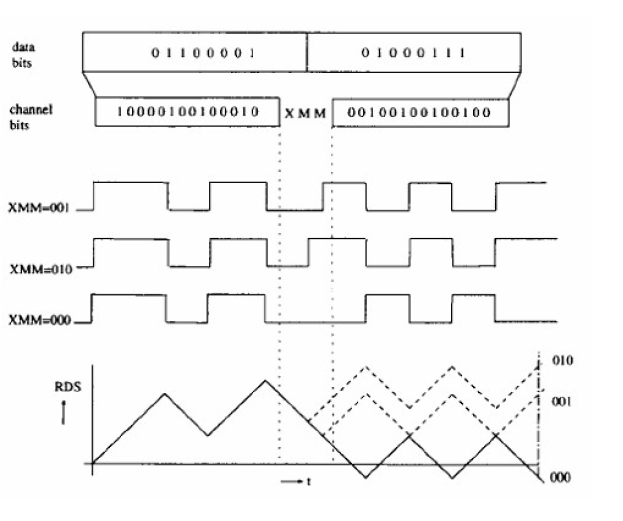
Il existe 267 codes EFM respectant la contrainte (2,10), mais lorsqu’on concatène deux codes EFM, il peut arriver que le résultat n’y réponde plus. La solution est d’insérer des bits de liaison (Merging bits). Ces bits de liaison seront choisis tels que la valeur absolue de la DSV (Digital
Sum Value) ou RDS (Running Digital Sum) soit la plus proche possible de 0. La RDS est un “indicateur de qualité de la réflexion” du disque qui, s’il est trop élevé ou trop bas, provoquera des erreurs de lecture.

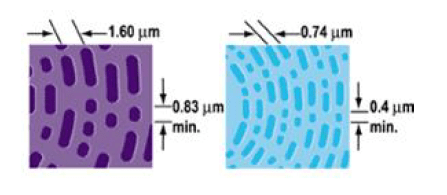
Le DVD (Digital Versatil Disc)

Le support de stockage est similaire au CD-Rom, mais le code correcteur d’erreurs est plus évolué et nécessite moins de bits.

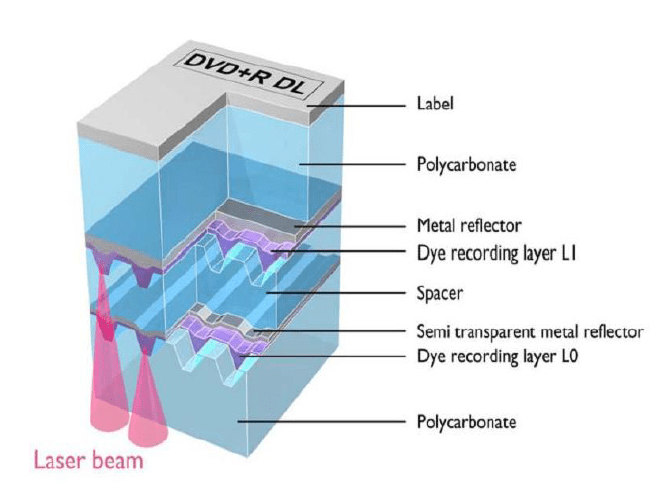
Le DVD DL (Double Layer)

En jouant sur la longueur d’onde du laser du lecteur (ou du graveur) et de la transparence des couches du disque, on peut lire (graver) plusieurs couches présentes sur le disque. Structure d’un DVD Double Couche [DaTARIUS Group]

Le HD-DVD

Au lieu d’utiliser le traditionnel laser rouge des graveurs conventionnels, on utilise ici le laser bleu, dont la longueur d’onde est plus courte.
Le codage utilisé est le ETM (Eight to Twelve Modulation). Il consiste en une table de correspondance entre les différents octets possibles et leur traduction sous la forme d’une suite de 12 bits. La contrainte est ici (1,10).

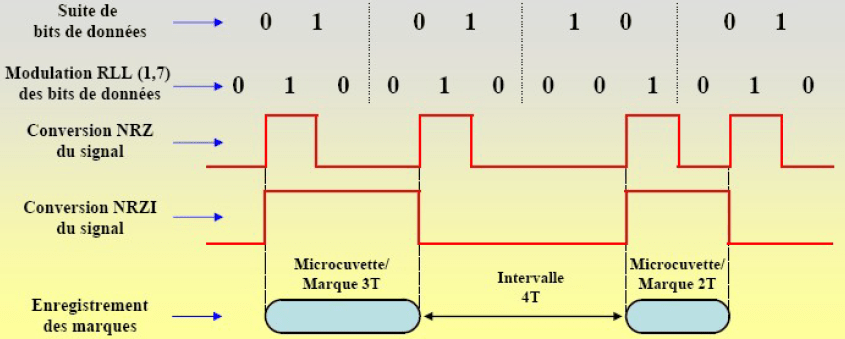
Le Blu-Ray

Il est lui aussi basé sur la technologie du laser bleu. Il possède dès lors une finesse de gravure égale à celle du HD-DVD. Ce support est plus performant en termes de capacité de stockage que le HD-DVD car le lecteur utilise une lentille plus évoluée. Le codage des données utilisé par le Blu-Ray porte le nom de 17PP et s’applique tel qu’illustré à la figure. Codage des informations sur un disque Blu-Ray [Source : Jean-José Wanègue].

Remarques :

Le thème étant en constante évolution, certaines remarques seront peut-être obsolètes dans un laps de temps plus ou moins court.

• A l’heure actuelle, tous les formats sont compatibles.
• Le problème de la cartouche du Blu-Ray fut supprimé grâce à une technologie mise au point par TDK (application d’une couche de polymère protectrice). Le disque étant protégé, il n’était donc plus nécessaire de conserver la cartouche.
• Si on compare les tailles des supports, le hd-dvd permet de stocker 30Go (2 couches de15Go), alors que le Blu-Ray autorise jusqu’à 50Go (2 couches de 25Go).
• En 2005, Toshiba a annoncé un Hd-DVD pouvant stocker 45 Go (3 couches). Au CES2 2006, TDK a présenté un prototype Blu-Ray de 100 Go (4 couches). Selon Sony, des recherches ont lieu pour créer des disques Blu-Ray de 8 couches et ainsi porter la taille du stockage à 200 Go.

Références:

• Support Compression et Stockage, Dumont Renaud

• Codage du texte, 2002

• American Standard Code for Information Interchange

• ASCII étendu

• ASCII

• Codage des caractères

• code ascii d’un caractère

• Le code ASCII

• TP4 – COMPTAGE DE CARACTÈRES – ARITHMÉTIQUE SUR LES CODES ASCII

• Codage et transmission des données dans un réseau

• L’enseignement du code informatique à l’école

• Introduction à l’informatique cours, G. Santini, J.-C. Dubacq, IUT de Villetaneuse

• Caractères, codage et normalisation – de Chappe à Unicode

• Tutoriel : Comprendre les encodages

• L’ENSEIGNEMENT DU CODE INFORMATIQUE À L’ÉCOLE Prémices d’un humanisme numérique congénital

Retour au menu