Objectifs
- Savoir la technique de discrétisation d’une fonction de transfert décrite dans le domaine de Laplace H(p)
- Savoir la fonction de transfert inverse d’un dérivateur du 1ère et 2nd ordre
- Savoir 3 techniques de discrétisation de la dérivée 1ère en utilisant les différences finies
- Etc.
Approximations de la dérivée première
Le polynôme du numérateur d’une fonction de transfert H(p)=Y(p)/X(p) est constitué par une combinaison linéaire de dérivation de l’entrée (voir la vidéo pour plus de détails).
Approximation par une différence finie en avance: Forward
h est la période d’échantillonnage
l’erreur absolue de l’approximation est proportionnelle à h/2
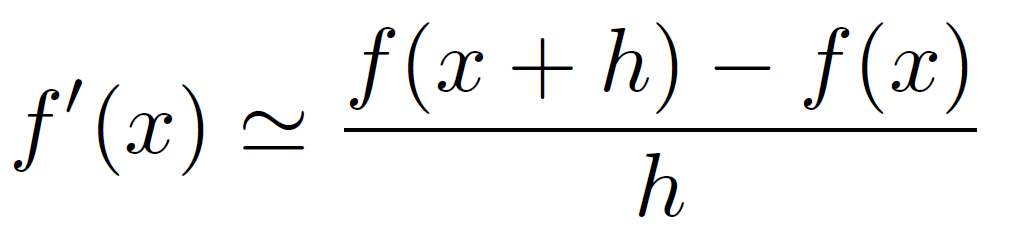
Approximation par une différence finie en retard: Backward
l’erreur absolue de l’approximation est proportionnelle à h/2
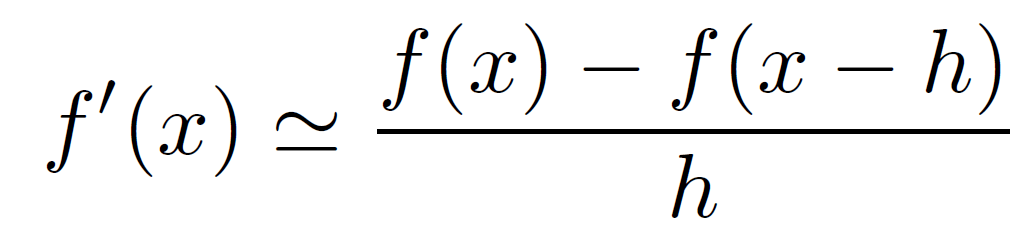
Approximation par une différence finie centrée: Center
l’erreur absolue de l’approximation est proportionnelle à h²/6
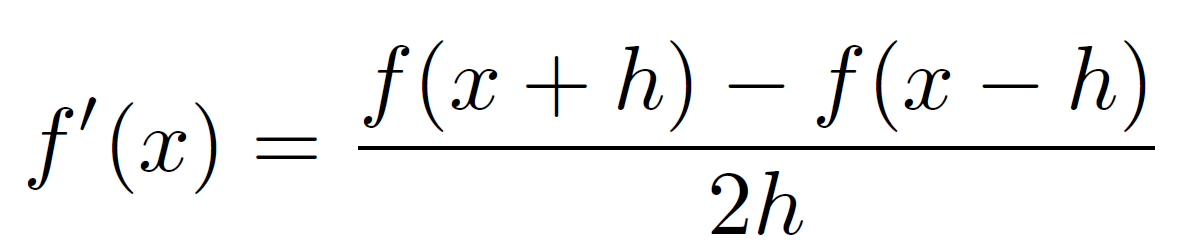
Méthode des différences finies
En analyse numérique, la méthode des différences finies est une technique courante de recherche de solutions approchées d’équations aux dérivées partielles qui consiste à résoudre un système de relations (schéma numérique) liant les valeurs des fonctions inconnues en certains points suffisamment proches les uns des autres. Lire la suite…
Implémentation avec Arduino
L’implémentation sur Arduino des trois approximations sera abordée dans la vidéo prochaine avec des exemples pratiques.

