Projets Matlab & Microcontrôleur #5: Jeu Labyrinthe avec Arduino et Matlab 1/2

Objectifs du projet:

Se familiariser avec le logiciel matlab
Se familiariser avec la programmation Arduino
Se familiariser avec la programmation des jeux
Choix de labyrinthe
Initiation au traitement d’image avec matlab
Et autres astuces pratiques

Outils de développement :

Matlab
Arduino
Carte électronique

Schéma de principe:

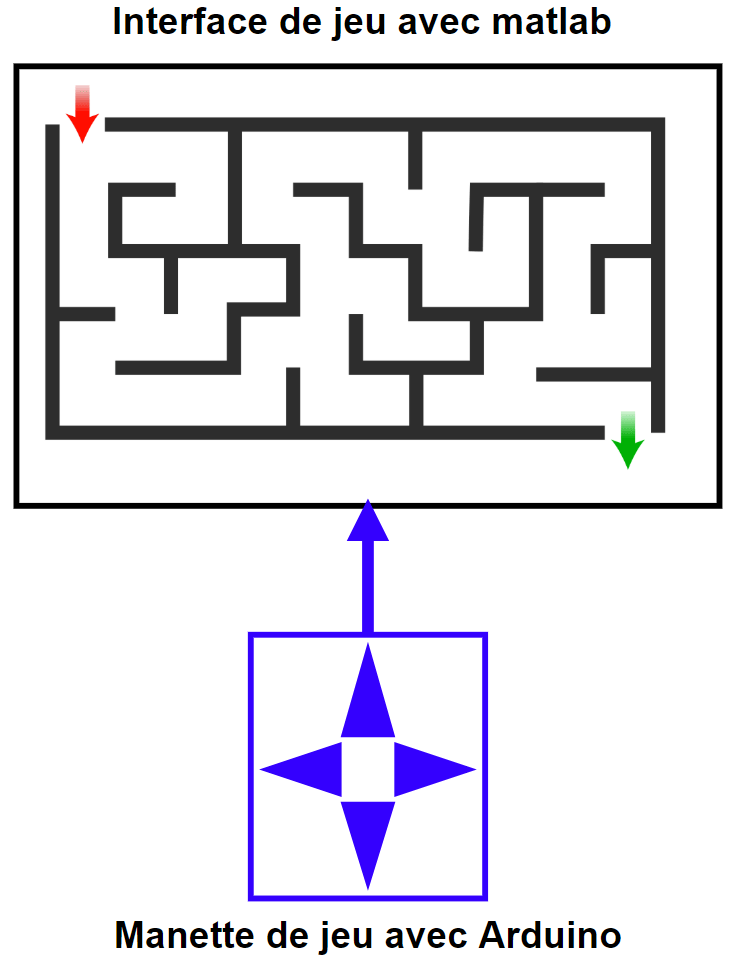
Fonctionnement partie 1/2

L’objectif du projet n’est pas de développer des jeux. Mais d’apprendre des notions de programmation en particulier savoir comment faire communiquer une carte Arduino avec le logiciel Matlab, savoir utiliser un émetteur/récepteur IR, etc. La présente partie du projet abordera la programmation purement Matlab d’un jeu labyrinthe. L’objectif du jeu et de se déplacer dans le labyrinthe d’un point A (départ) au point B (destination) au moindre coût. En effet, le compteur incrémente pour chaque déplacement « correct » de l’utilisation, une fausse manœuvre (déplacement dans une zone interdite, joueur hors zone du labyrinthe) lui faire augmenter le compteur d’une pénalité. La valeur de la pénalité est fixée par l’utilisateur (Exemple : Augmenter le compteur de 5, 10, etc.). Lorsque le jureur arrive à la destination, il doit avoir un score minimal.

Comment ça marche la manette du jeu ?

La manette du jeu est constituée de quatre boutons :

Haut (Up) : Déplacer le joueur d’un pas en haut et incrémenté le compteur d’une unité
Bas(Donw) : Déplacer le joueur d’un pas en bas et incrémenté le compteur d’une unité
Gauche (Left) : Déplacer le joueur d’un pas à gauche et incrémenté le compteur d’une unité
Gauche (Right) : Déplacer le joueur d’un pas à droite et incrémenté le compteur d’une unité

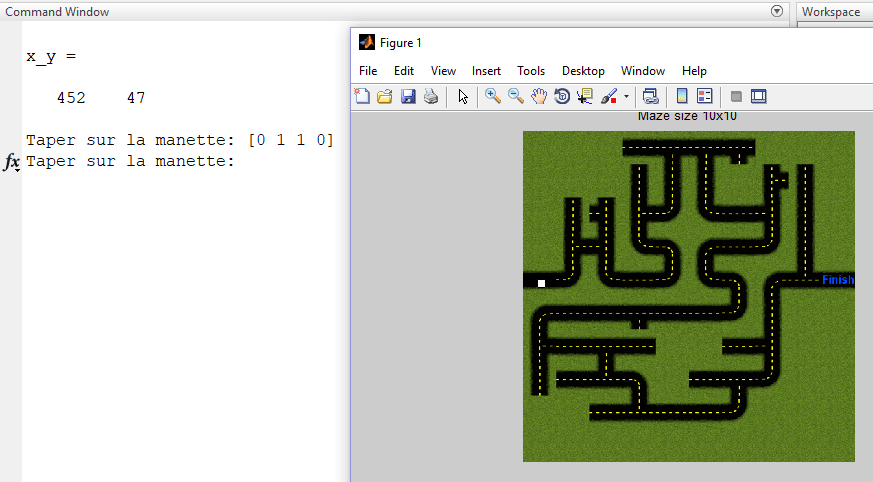
Lorsque on débute le jeu. Je joueur est positionner dans la position initiale. Le programme matlab demande à l’utilisateur d’entrée un vecteur de taille 4. Chaque valeur est affectée à un déplacement (haut, bas, droit et gauche). Le vecteur doit contenir uniquement des « 0 » ou « 1 ».

« 1 » : Indique l’activation du déplacement qui lui correspond
« 0» : Déplacement inactif

Exemples :

[0 0 0 0 ] : Joueur en attente (aucune déplacement)
[1 0 0 0 ] : Déplacement d’un pas vers bas
[0 1 0 0 ] : Déplacement d’un pas vers le haut
[0 0 1 0 ] : Déplacement d’un pas vers la droite
[0 0 0 1 ] : Déplacement d’un pas vers la gauche

Note : Lorsque la somme des valeurs des déplacement est >1, le joueur reste en état d’attente (Ex : [1 1 0 0], [1 1 1 1], [1 10 45 0] , etc.).

Le joueur

Le joueur dans le labyrinthe est un carré blanc de taille fixe qui se déplace en fonction du bouton actionné par l’utilisateur. Le joueur est de taille fixe égale à NxN, la valeur de N en pixels est réglable par l’utilisateur (Exemple N=20 pixels)

Comment générer un labyrinthe avec Matlab ?

Le générateur de labyrinthe génère un labyrinthe composé de plusieurs types de composants. Le labyrinthe est généré par un échange itératif aléatoire de pièces interchangeables ainsi que par des pièces jointes aléatoires de nouvelles pièces. Le designer a ajouté des fonctions permettant d’afficher et / ou d’enregistrer le labyrinthe généré sous forme d’image. Le code est relativement lent, mais il est censé être davantage une approche de la génération de labyrinthe que toute autre chose. Vous trouverai le code ICI dont on aura besoin pour la suite du projet.

Décompresser le dossier téléchargé. Ouvrir le script «example_script.m » dans le dossier « Maze_generator_v1 ». L’exemple permet de générer trois labyrinthes de taille 10×10, 20×20 et 20×30. Ci après le contenu du script. On distingue quatre paramètres et deux fonctions essentiels dans le script:

sz: la faille du labyrinthe
tile_sz: longueur de la fenêtre d’affichage. La taille de l’image de sortie égale (sz*tile_sz)x(sz*tile_sz)
tangling_steps : Paramètre interne du générateur aléatoire (lorsque la valeur est importante, le labyrinthe devient complexe)
growing_steps : Paramètre de croissance du labyrinthe (lorsque la valeur est importante, le labyrinthe devient complexe)

Les fonctions:

Maze_gen(): Fonction génératrice du labyrinthe
Plot_maze(): Convertir une labyrinthe en une image RGB

Script example_script.m

function example_script

% %  example_script
%
% This script is an example of the proper usage of the Maze_gen
% and the Plot_maze functions

sz=10;
tile_sz=100;
tangling_steps=200;
growing_steps=800;

[elements,t_set] = Maze_gen( sz,tangling_steps,growing_steps );
img_maze = Plot_maze( elements,t_set,tile_sz );

figure
imshow(img_maze)
title('Maze size 10x10')

sz=20;
tile_sz=100;
tangling_steps=400;
growing_steps=1600;

[elements,t_set] = Maze_gen( sz,tangling_steps,growing_steps );
img_maze = Plot_maze( elements,t_set,tile_sz );

figure
imshow(img_maze)
title('Maze size 20x20')

sz=30;
tile_sz=100;
tangling_steps=400;
growing_steps=2600;

[elements,t_set] = Maze_gen( sz,tangling_steps,growing_steps );
img_maze = Plot_maze( elements,t_set,tile_sz );

figure
imshow(img_maze)
title('Maze size 30x20')
end

Résultats d’affichages du script

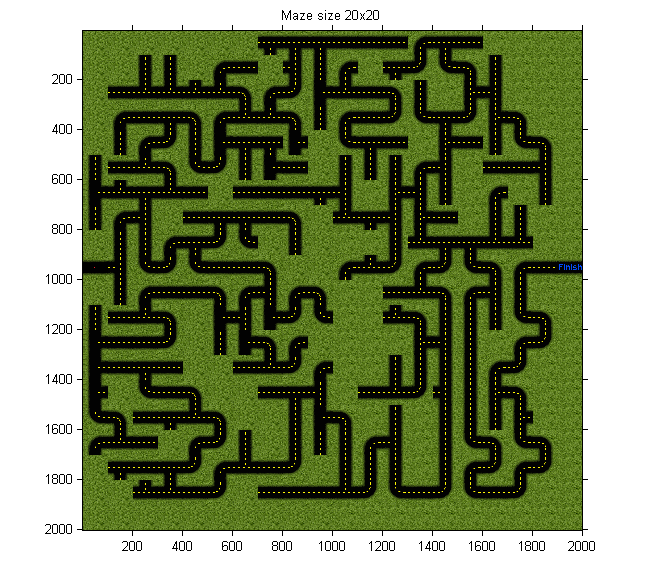
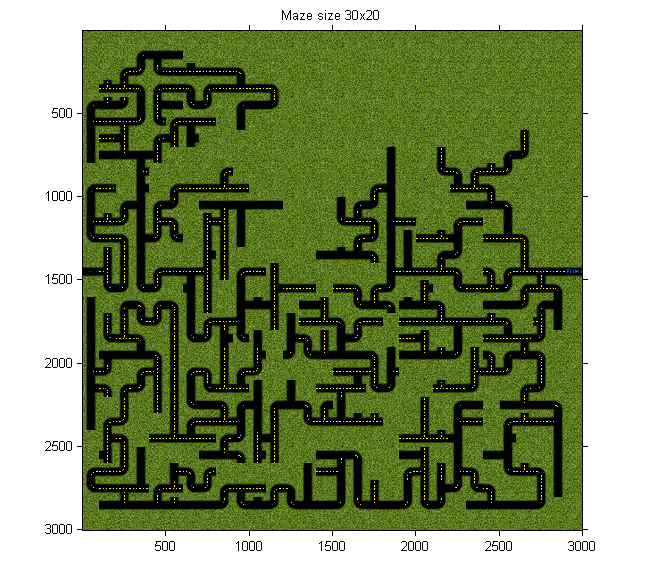
Exemple 2: Script LabynGen.m

clear all; close all; clc;

%% Paramètres du Labyrinthe

% Params taille d'affichage
sz=10;
tile_sz=100;

% Params générateurs aléatoires 
tangling_steps=300;
growing_steps=900;

%% Génération 

% Labyrinthe 1: 10x10
[elements,t_set] = Maze_gen( sz,tangling_steps,growing_steps);
img_maze = Plot_maze( elements,t_set,tile_sz);

% Labyrinthe 2: 10x10
[elements,t_set] = Maze_gen(1.5*sz,tangling_steps,growing_steps);
img_maze_1 = Plot_maze( elements,t_set,tile_sz);

% Labyrinthe 3: 10x10
[elements,t_set] = Maze_gen(2*sz,tangling_steps,growing_steps);
img_maze_2 = Plot_maze( elements,t_set,tile_sz);

% Labyrinthe 4: 10x10
[elements,t_set] = Maze_gen(2.5*sz,tangling_steps,growing_steps);
img_maze_3 = Plot_maze( elements,t_set,tile_sz);


%% Affichage

figure(1); imshow(img_maze); title('Maze size 10x10'); axis square; axis on;
figure(2); imshow(img_maze_1); title('Maze size 15x15'); axis square; axis on;
figure(3); imshow(img_maze_2); title('Maze size 20x20'); axis square; axis on;
figure(4); imshow(img_maze_3); title('Maze size 25x25'); axis square; axis on;

Comment positionner le joueur au début du labyrinthe ?

Le dossier Maze_Generator_V1/pics _0 contient les imagettes constituant les briques de base du labyrinthe. Elles sont assemblées par l’algorithme du générateur aléatoire du labyrinthe. On constate la présence de 14 images au format .bmp de dimensions 100×100. L’image de début contient le mot « start » et « finish » pour la fin du labyrinthe. Lorsqu’on génère un labyrinthe on obtiendra les deux mots au début et à la fin, mais comment peut-on obtenir les coordonnées du début sachant qu’elles variées pour chaque itération ?

L’astuce consiste à faire une modification dans l’imagette de début, on supprime le mot « finish » puis on met à la place un pixel rouge dont la valeur est connue par l’utilisateur. Cette valeur sera par la suite localisée par le programme. En effet, aucun pixel ne dispose de la couleur rouge dans le labyrinthe, une simple recherche de la valeur nous dévoilera les coordonnées du début.

Fonction de recherche GetPixel.m

La nouvelle fonction GetPixel() prend en entrée l’image RGB du labyrinthe et la valeur du pixel rouge au format RGB. Elle retourne les coordonnées (x0, x0) du début). Le joueur sera ensuite placé autour du (x0, y0). Ci-dessous la définition de GetPixel().

function x_y = GetPixel( im_in_RGB, pix_val)

% R=236;
% G= 28;
% B=36;
% [236 28 36]

R=pix_val(1);
G=pix_val(2);
B=pix_val(3);
r=0;

[m, n, p]=size(im_in_RGB);
for i=1:m
    for j=1:n
        if im_in_RGB(i,j,1)==R && im_in_RGB(i,j,2)==G && im_in_RGB(i,j,3)==B
            x_y=[i, j];
            i=m; j=n;
            r=100;
            break;
        end
    end
end
if r~=100
    x_y=[1,1];
end

Comment séparer entre la zone du jeu et la zone hors-jeu ?

Lorsqu’on déplace le joueur dans le labyrinthe, il se peut que le joueur se retrouve dans une zone hors labyrinthe (zone verte). La manette du jeu permet de se déplacer dans les quatre directions vers la cible. Nous avons expliqué que le déplacement vers la zone interdite induite l’augmentation du compteur (perte du score). La question reste à savoir comment faire la différence entre les deux zones ?

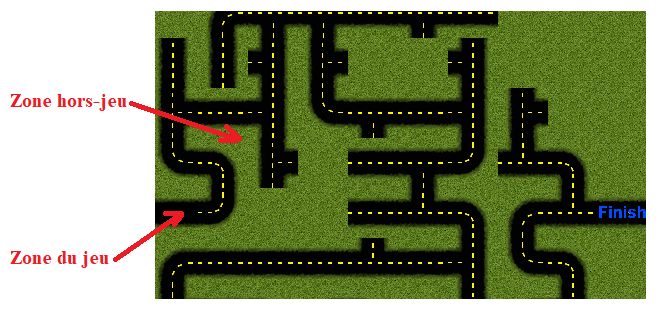
La technique consiste à calculer la valeur moyenne des pixels du bloc NxN dans lequel se retrouve le joueur. La valeur moyenne sera ensuite comparée avec la valeur moyenne de la zone interdite (zone verte). Si la valeur moyenne dépasse celle de la zone, alors on se retrouve dans la zone, sinon le joueur est dans le labyrinthe. En effet, après analyse de la valeur moyenne à l’intérieur du labyrinthe, on conclut que la valeur moyenne du bloc NxN est relativement faible, car le labyrinthe est composé des canaux noirs (pixels nuls) avec des traits jaunes (pixels non nuls). En moyenne la valeur est faible par rapport à la zone interdite. La valeur moyenne sera calculée après transformation de l’image RGB (3 D) en image aux niveaux de gris (2 D) pour des raisons de simplification. Ci-dessous l’extrait du code :

...
% Extraction du bloc NxN
im_0= img_maze0(Start_y:Start_y+N-1,Start_x:Start_x+N-1,:);
 
% Conversion RGB => Gray
im_0=rgb2gray(im_0);
 
% Caclul de la valeur moyenne
mean_pixel=mean(im_0(:));
 
% Gestion du compteur: Incrémentation ou Pénalité
if(mean_pixel < Seuil_outZone)
    % Zone du jeu => Incrémentation
else
    % Hors-jeu => Pénalité
end
...

Programme principal Matlab (main.m)

clear all; close all; clc;

% Params Labyrinthe
sz=10;
tile_sz=100;
tangling_steps=300;
growing_steps=900;

% Génération LABY
[elements,t_set] = Maze_gen( sz,tangling_steps,growing_steps);
img_maze = Plot_maze( elements,t_set,tile_sz);

% Taille du joueur  NxN
N=20;

% Déplacement en pixel
Pas=round(N/2);

% Coordonnées de la position initiale du joueur (x0, y0)
img_maze0=img_maze; im_rgb=((im2uint8(img_maze0)));
pix =[236 28 36];
x_y=GetPixel(im_rgb, pix)
Start_y_0=x_y(1);Start_y=Start_y_0;
Start_x_0=x_y(2); Start_x=Start_x_0;

% Manette
Manette=ones(1,4);
Seuil_outZone=0.3;

% Positionner le joueur sur (x0, y0)
img_maze0(Start_y_0:Start_y_0+N-1,Start_x_0:Start_x_0+N-1,:)=128*ones(N,N,3);
im_affich=imresize(img_maze0,[512 512]);
imshow(im_affich); title('Maze size 10x10'); axis square;

% Compteur pas vers la cible
Cmp_cible=0;
Out_zone_pinal=5;
figure(1);
while(1)
    % Lecture des coordonnées
    while(sum(Manette)>1)
        Manette=input('Taper sur la manette: ');
        Manette=mod(Manette,length(img_maze0));
    end;
    
    % Extraction des valeurs
    Down =Manette(1);
    Up=Manette(2);
    Right =Manette(3);
    Left=Manette(4);
    
    % Déplacement
    if Up~0
        Start_y=Start_y_0+Pas;
    elseif Down~0
        Start_y=Start_y_0-Pas;
        if Start_y <=0
            Start_y=1;
        end;
    end;
    if Right~0
        Start_x=Start_x_0+Pas;
    elseif Left~0
        Start_x=Start_x_0-Pas;
        if Start_x <=0
            Start_x=1;
        end;
    end;
    
    %  Calcul de la valeur moyenne de la position actuelle
    
    % Extraction du bloc NxN
    im_0= img_maze0(Start_y:Start_y+N-1,Start_x:Start_x+N-1,:);
    
    % Conversion RGB => Gray
    im_0=rgb2gray(im_0);
    
    % Caclul de la valeur moyenne
    mean_pixel=mean(im_0(:))
    
    % Gestion du compteur: Incrémentation ou Pénalité
    if(mean_pixel < Seuil_outZone)
        % Affichage
        img_maze0(Start_y:Start_y+N-1,Start_x:Start_x+N-1,:)=128*ones(N,N,3);
        im_gray=im2uint8(imresize(img_maze0,[512 512]));
        imshow(rgb2gray(im_gray)); title('Maze size 10x10'); axis square;
        
        % Mise à jour
        Start_y_0=Start_y;
        Start_x_0=Start_x;
        Cmp_cible=Cmp_cible+1
    else
        Cmp_cible=Cmp_cible+Out_zone_pinal
    end
    
    % Délai & Init
    pause(0.5);
    Manette=ones(1,4);
    img_maze0=img_maze;
end