Objectifs
- Savoir l’importance de la fonction tanh(x)
- Savoir les caractéristiques du tanh(x)
- Les effets de non linéarité
- Analyse fréquentielle de la fonction tanh(f(x)
- Etude des exemples pratiques.
Exemples d’Applications
- Bloc de saturation dans un régulateur (systèmes asservis)
- Écrêteur, limiteur du signal
- Fonction d’activation dans les réseaux de neurones
- Comparateur : Passage d’un signal analogique en un signal logique
- Etc.
Programme Arduino
clear all; close all; clc
%%
% Matlab #15: La Fonction Tengente Hyperbolique tanh()
% www.Electronique-Mixte.fr
%% Objectifs:
% 1. Savoir l'importance de la fonction tanh(x)
% 2. Savoir les caractéristiques du tanh(x)
% 3. Les effets de non linéarité
% 4. Analyse fréquentielle de la fonction tanh(f(x)
% 5. Etudes des exemples pratiques.
% La fonction tanh(x)
% tanh(+Inf)=>1
% tanh(-Inf)=>-1
% tanh(x~0)=>x
%% Signal temporel
% Génération du signal s(t)=sin(t)
f0=1; t0=1/f0; N=1e3; n=2;
t=linspace(-n*t0,n*t0,N);
A=10; s_t=A*sin(2*pi*f0*t);
% La fonction tanh()
%s_tanh=tanh(t);
s_tanh=tanh(s_t);
s_tanh1=sign(s_t).*((s_t>0)|(s_t<0));
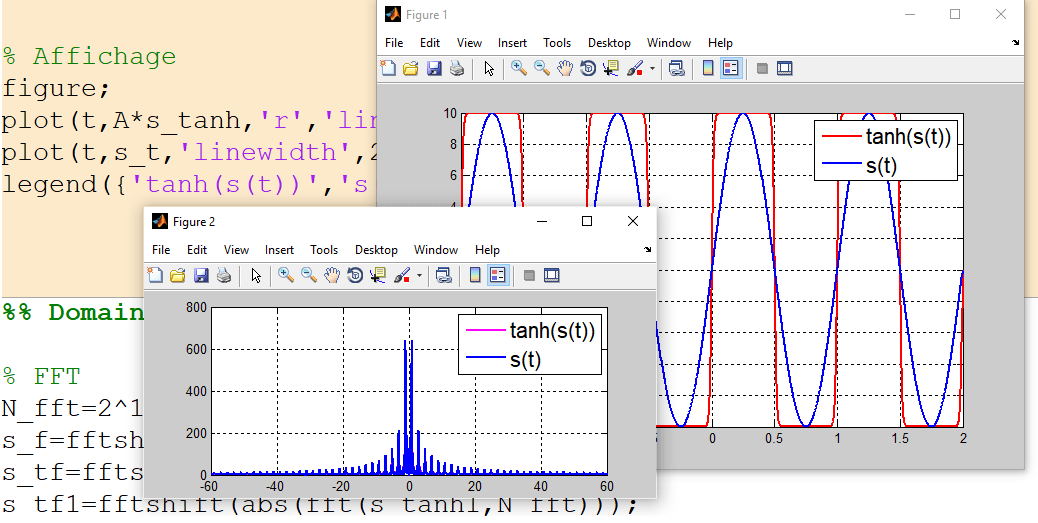
% Affichage
figure;
plot(t,s_tanh,'r','linewidth',2); grid on; hold on;
plot(t,s_t,'linewidth',2); grid on; hold on;
legend({'tanh(s(t))','s(t)'},'fontsize',16);
%% Domain fréquentiel
% FFT
N_fft=2^14;
s_f=fftshift(abs(fft(s_t,N_fft)));
s_tf=fftshift(abs(fft(s_tanh,N_fft)));
s_tf1=fftshift(abs(fft(s_tanh1,N_fft)));
% Affichage
ts=t(2)-t(1); fs=1/ts;
f=linspace(-fs/2,fs/2, N_fft);
figure;
%plot(f,A*s_tf,'r','linewidth',2); grid on;hold on;
plot(f,s_tf,'m','linewidth',2);grid on;hold on;
plot(f,s_tf1,'linewidth',2);
%legend({'tanh(s(t))','s(t)'},'fontsize',16);
nn=60;xlim([-nn*f0 nn*f0]);
Retour à l'Aceuil Matlab


