Filtre analogique ajustable avec microcontrôleur

Objectifs

Comprendre le principe de fonction d’un filtre passe-bas
Savoir dimensionner un filtre passe-bas 2^nd ordre
Savoir utiliser un potentiomètre numérique
Savoir créer un signal Sinusoïdal à partir d’un signal carrée
Etc.

Fonctionnement

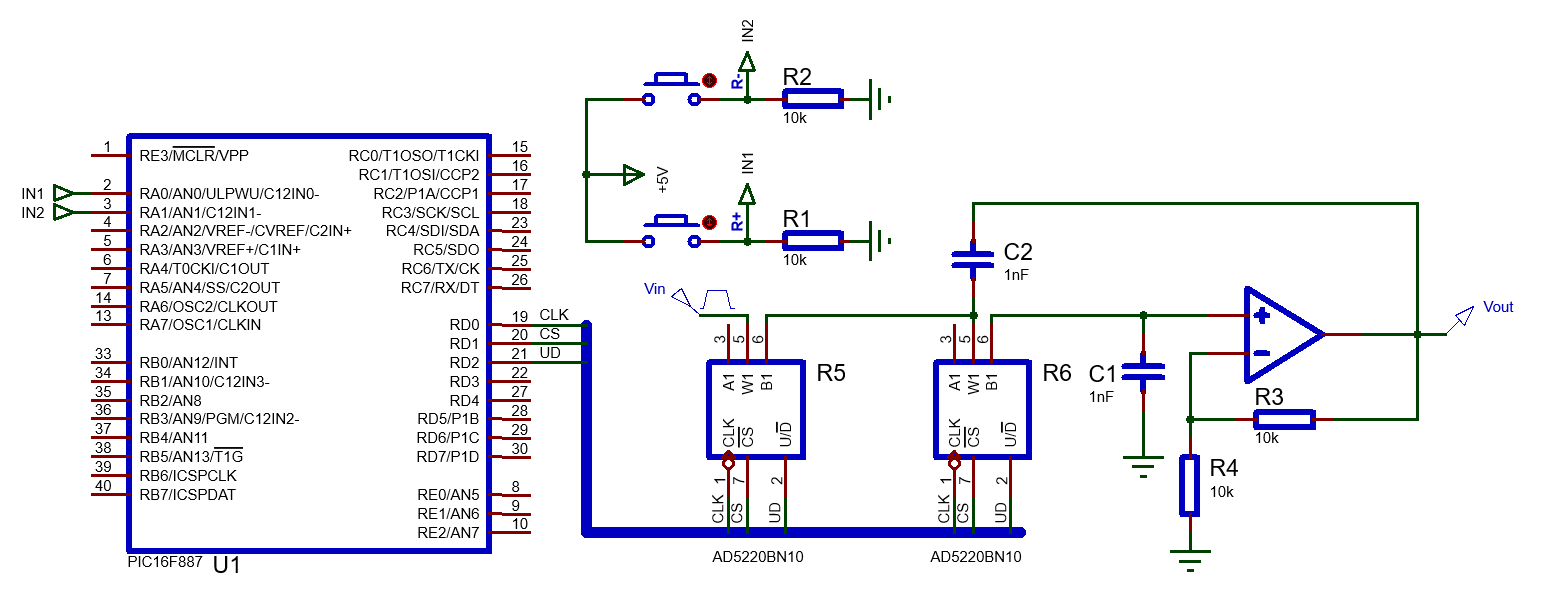
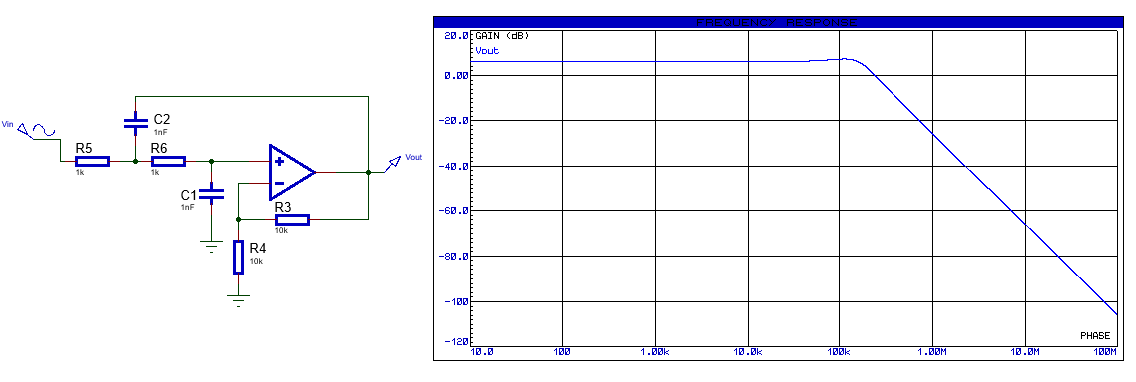
Le montage est un filtre passe-bas 2nd ordre ayant une bande passante ajustable par le microcontrôleur. Il composait de deux potentiomètres numériques identiques et ajustables par le µc via la liaison sérient. La valeur des potentiomètres agis sur la fréquence de coupure du filtre ainsi le dépassement. En revanche, le gain il reste constant. On utilise la cellule de Sallen & Key passe-bas basé sur le circuit RC et un amplificateur opérationnel (OAP). Le premier µc joue le rôle d’un émetteur : Il envoie l’ordre d’augmenter ou réduire la bande passante. Le deuxième microcontrôleur joue le rôle du récepteur : Il reçoit la commande et la transmise au filtre pour ajuster la bande passante.

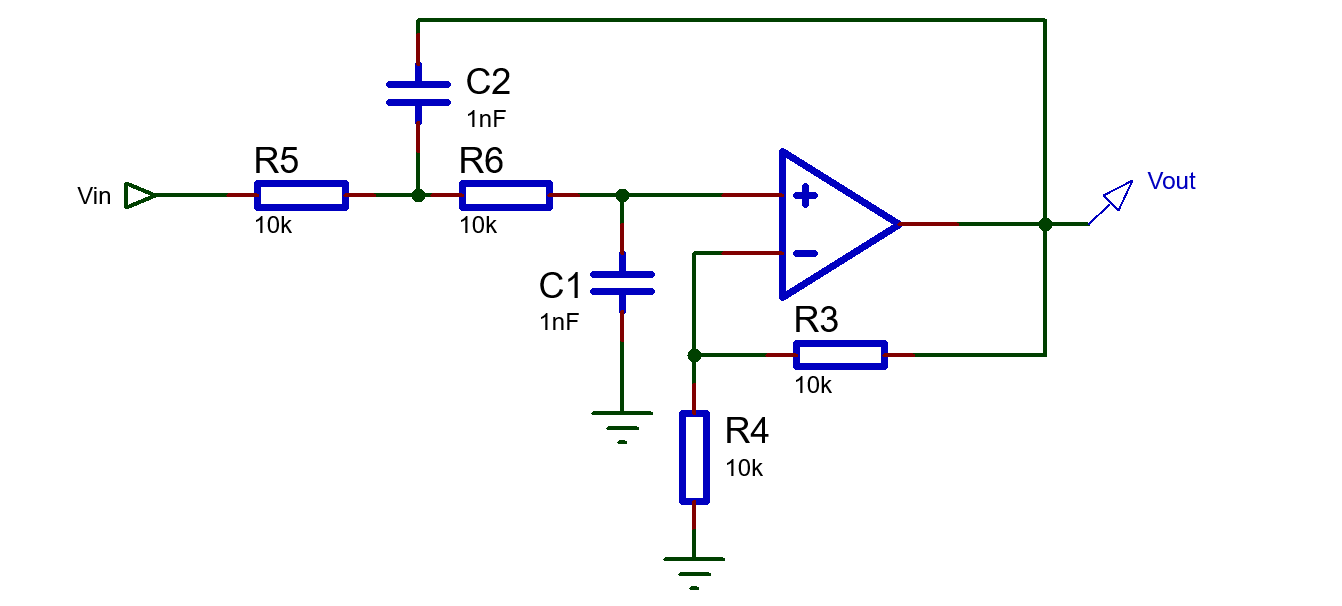
Filtre passe-bas à base de l’architecture Sallen & Key

Le filtre passe-bas est composé de deux condensateurs C1 et C2 et les résistances R5 et R5. Le gain du filtre est fixé par les résistances R3 et R4. C-après la fonction du transfert du filtre ainsi les paramètres qui le caractérise. On considère pour des raisons de simplification que R5=R6=R, C1=C2=C.

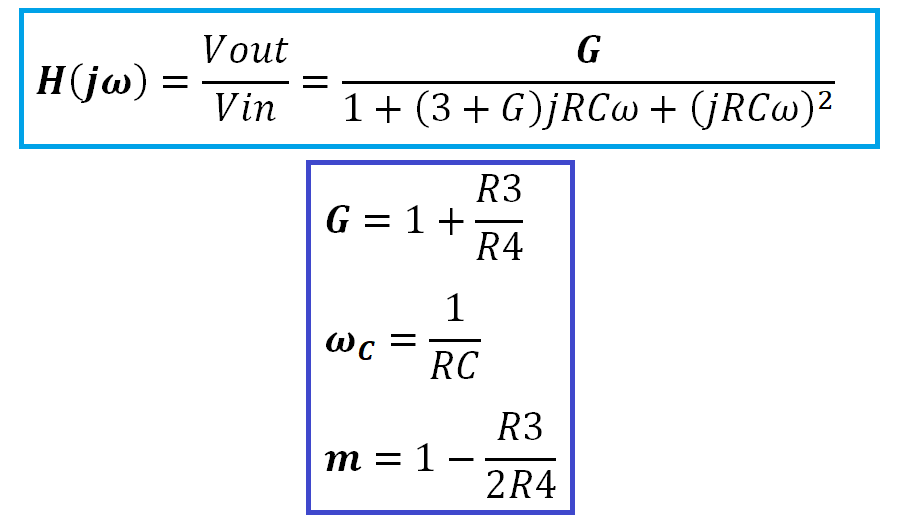
H: La fonction du transfert du filtre dans le régime harmonique
G: Gain du filtre, il ne dépend que des résistances R3 et R4
Wc: La pulsation de coupure est l’inverse du produit RC
m: Coefficient d’amortissement, il indique la présence du dépassement (m< 0.7) ou non

Calcul théorique

R3=R4 ==> G=1+1=2
G(dB)=20log(2)=6.02 dB
Wc=1/RC=10E+5 rad/s => fc=15.91 kHz
m=1-1/2=0.5<0.7 ==> Présence de dépassement

Simulation (R5=R6=10k)

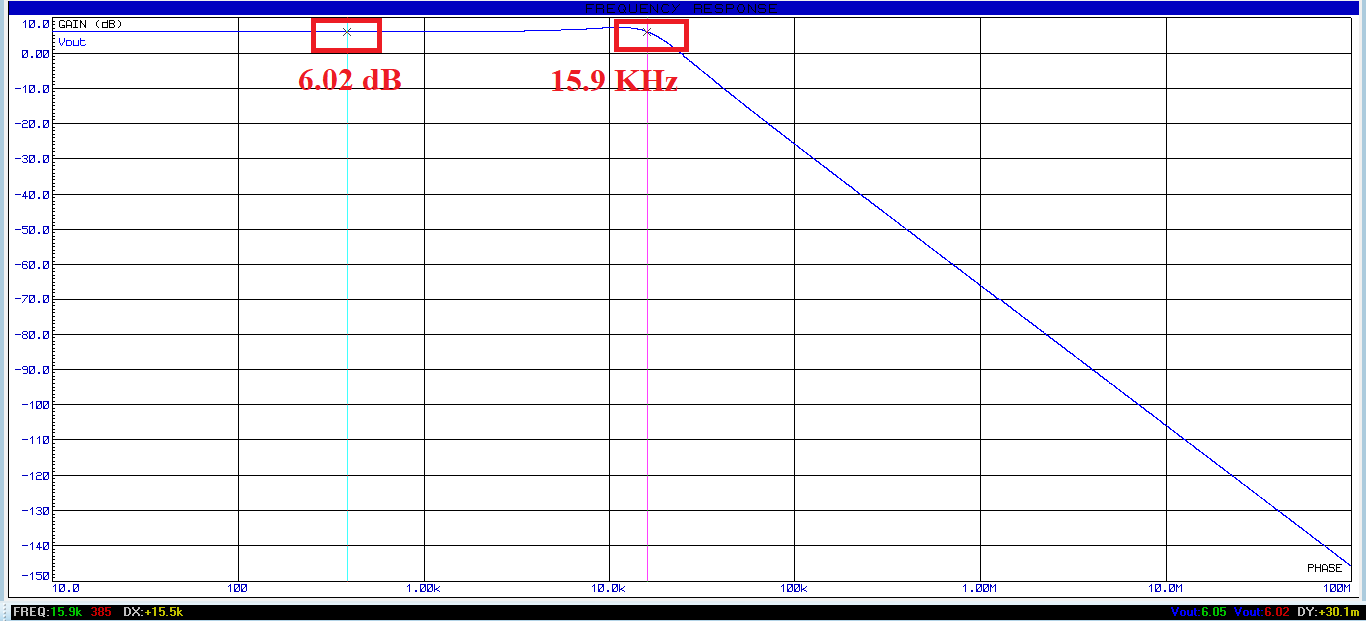
En utilisant la réponse fréquentielle du montage qui permet de simuler la fonction du transfert du montage en fonction de la fréquence. Dans notre exemple, la fréquence maximale est limitée à 100 MHz. Ci-dessous les résultats obtenus:

Gains statique : 6.02 dB
Fréquence de coupure : 15.9 HKz

Les résultats sont conformes en comparaison avec les valeurs théoriques

Simulation (R5=R6=R=1k)

Division par 10 de la résistance R (R=1k au lieu de 10k) implique une multiplication de la fréquence de coupure par 10 = 159 KHz.

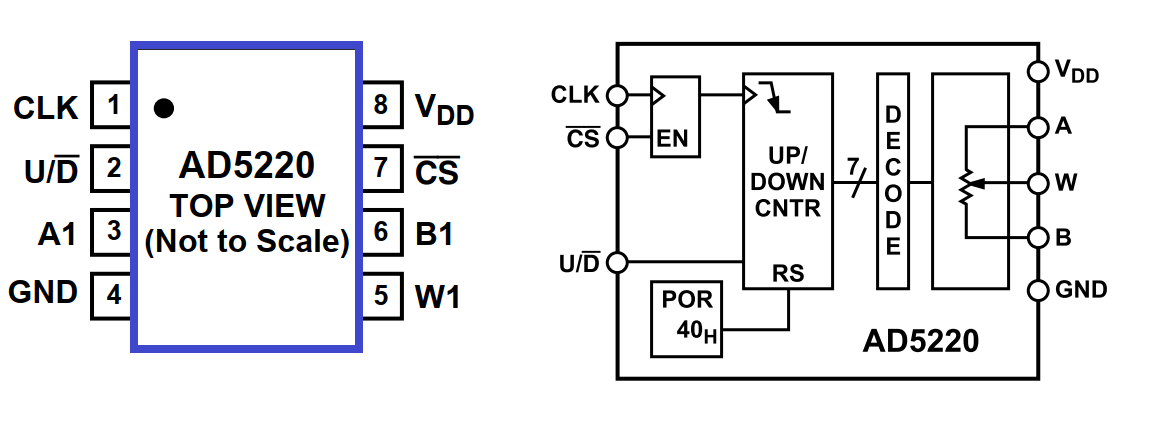
Potentiomètre numérique AD5220

Le circuit AD5220 est un potentiomètre numérique facilement contrôlable. De valeur égale à 10k (50k ou 100k) avec une résolution sur 7 bits (128 combinaisons possibles de la valeur totale : 128*10k/128=128* 78.125). Autrement dit on peut incrémenter (ou décrémenter) la valeur de la résistance d‘un pas égal à 78.125 Ohm. Ci-dessous les caractéristiques techniques du circuit ainsi la description des broches.

128 positions : Compteur 7 bits
Compteur/Décompteur intégré
Commande par horloge externe
Résistance : 10k
Alimentation : -0.3 à 7V
Courant à la borne du potentiomètre : +/-20mA
Datasheet AD5220

Pin No.	Name	Description
1 2 3 4 5 6 7 8	CLK U/D A1 GND W1 B1 CS VDD	Serial Clock Input, Negative Edge Triggered UP/DOWN Direction Increment Control Terminal A1 Ground Wiper Terminal Terminal B1 Chip Select Input, Active Low Positive Power Supply

Les signaux de contrôle

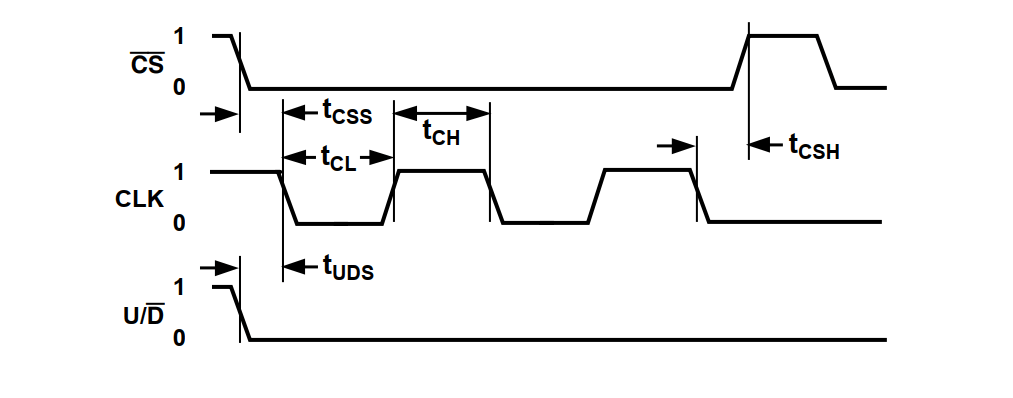
Le circuit dispose de trois signaux d’entrées pour l’ajustement de la résistance interne. Ci-dessous les chronogrammes et les étapes à suivre pour le contrôle de ce dernier :

Par défaut le signal CS=1 (logique négative), on met CS = 0 afin d’activer le composant
On position le signal U/D à zéro ou à 1 en fonction de l’opération désirer : Incrémentation de la valeur (Up, U/D=1) ou décrémentation (Down, U/D=0)
Le signal d’horloge CLK est égal à « 1 » par défaut, on le remet à 0 afin de valider l’opération.
On remet les signaux par défaut : CS= 1, CLK=1
On recommence le cycle

Schéma du filtre ajustable

On remplace les résistances R5 et R6 par deux potentiomètres numériques AD5220 branchés en parallèles
CLK => D0, CS => D1, U/D => D2
Boutons poussoirs: R(+): Incrémentation de la résistance, R(-): Décrémentation
R(+) => RA0, R(-) => RA1

Comment convertir un signal carré en signal sinusoïdal ?

Un signal carré est un assemblage (la somme) de plusieurs signaux sinusoïdaux avec des fréquences et amplitudes différentes. Si on arrive à sélectionner une fréquence parmi d’autres, on obtiendra un signal sinusoïdal pur. En effet, la transformée de fourrier d’un signal carrée indique la présence des harmoniques multiples de la fréquence fondamentale du signal f0 (A0, 1f0, 3f0, 5f0, etc.) (voir les figures ci-dessous). Le filtre permet de supprimer les harmoniques 3f0, 5f0, etc. et maintenir la fréquence fondamentale f0 et la composante DC A0.

La FFT du signal Vin(t) (avant le filtrage – entrée du filtre)

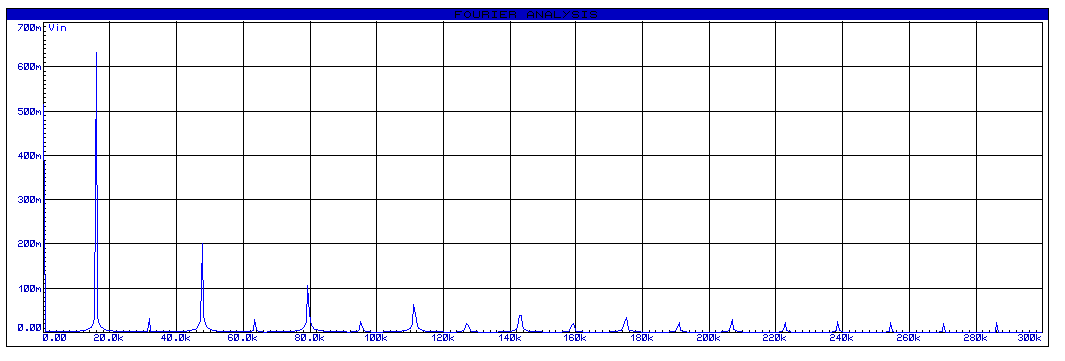
La FFT du signal Vout(t) (après le filtrage – sortie du filtre)

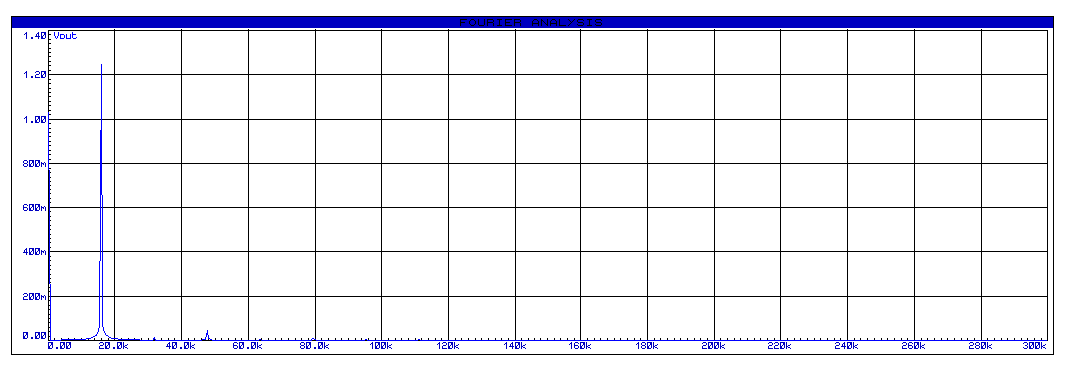
Simulation du montage

On considère le montage précédent avec R5=R6=10k fixent. On injecte un signal carré de fréquence égale à la fréquence de coupure du filtre. D’après les simulations, on obtient un signal presque sinusoïdal à la sortie du filtre avec un déphasage (retard) par rapport au signal carré. Par conséquent, le filtre à bien illuminer les harmoniques secondaires constituant le signal d’entrée et garder uniquement la fréquence fondamentale. On constate également la présence de la composante continue dans le signal de sortie : Le filtre a un comportement passe-bas, donc on présence l’ensemble de la bande basse du signal y compris la fréquence nulle (composante DC).

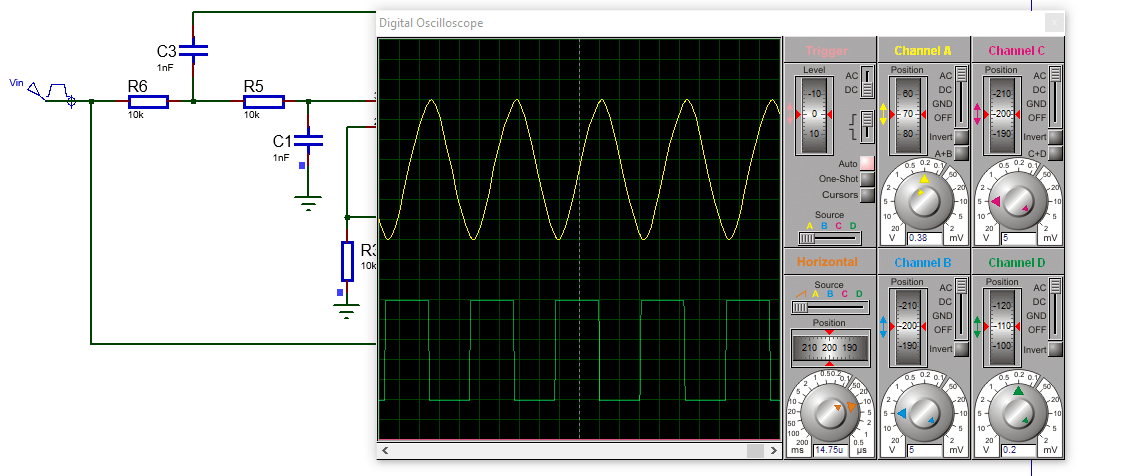
On peut réduire la composante DC en utilisant un condensateur à la sortie ou un filtre passe-bande à la place du filtre PB.

Programme MikroC

#include <built_in.h>

// LCD module connections
sbit AD5220_CLK at RD0_bit;
sbit AD5220_CS at RD1_bit;
sbit AD5220_UP at RD2_bit;

void main()
{
     // Configure AN pins as digital
     ANSEL  = 0;
     ANSELH = 0;

     // Port A en entrée
     TRISA=0xFF;

     // Configuration en sortie des ports
     TRISD=0;
     
     // Initialisation AD5220
     PORTD=0xFF;
     AD5220_CLK=1;
     AD5220_CS=1;
     AD5220_UP=1;

     while(1)
     {
      // UP Counter
      if (Button(&PORTA, 0, 1, 1))
      {
         // Activation du circuit AD5220
         AD5220_CS=0;
         delay_ms(10);
         
         // Mode incrémentation
         AD5220_UP=1;
         delay_ms(10);
         
         // Activation de l'horloge
         AD5220_CLK=0;
         delay_ms(10);
         
         // Initialisation AD5220
          AD5220_CLK=1;
          AD5220_CS=1;
          AD5220_UP=1;
      
         // Tempo cycle
         Delay_ms(100);
      }
      
      // Down Counter
      if (Button(&PORTA, 1, 1, 1))
      {
         // Activation du circuit AD5220
         AD5220_CS=0;
         delay_ms(10);

         // Mode décrémentation
         AD5220_UP=0;
         delay_ms(10);

         // Activation de l'horloge
         AD5220_CLK=0;
         delay_ms(10);
         
         // Initialisation AD5220
          AD5220_CLK=1;
          AD5220_CS=1;
          AD5220_UP=1;

         // Tempo cycle
         Delay_ms(100);
      }
      
      // Initialisation AD5220
      AD5220_CLK=1;
      AD5220_CS=1;
      AD5220_UP=1;

     }
}

Autres filtres

Voir le logiciel de synthèse des filtres actifs dans la rubrique « logiciel »

Téléchargement

Retour à l’accueil MikroC