Projet électronique #18: Wattmètre avec Arduino

 

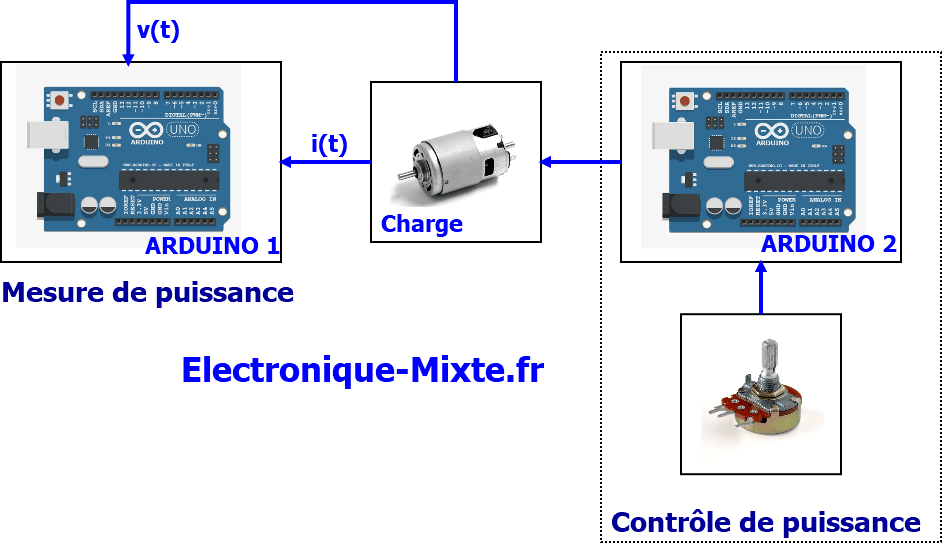
Objectifs du projet : répondre aux interrogations suivantes :

1. Comment calculer la puissance électrique ?
2. Comment mesurer le courant à la borne dune charge avec Arduino ?
3. C’est quoi la différence entre la puissance instantanée et la puissance moyenne ?
4. C’est quoi la formule de la puissance instantanée et la puissance moyenne ?
5. Comment mesurer la puissance d’une charge avec Arduino ?
6. Etc.

Rappels des cours

1. Puissance moyenne en régime sinusoïdal force
2. Énergie et puissance électrique
3. La puissance en régime sinusoïdal forcé
4. Mesure de puissance en électricité
5. Puissance en régime sinusoïdal
6. Puissance P.E.P. et puissance moyenne
7. Puissances
8. Travail et puissance

Le courant au démarrage du moteur (PIC au démarrage)

Les moteurs à courant continu (ou alternatif) sont caractérisés par une demande du courant important au démarrage pour une courte durée (de l’ordre des dizaines ou centaines de millisecondes) afin de mettre le système en mouvement. Pendant le démarrage (régime transitoire), le courant au démarrage est inversement proportionnel à la résistance R (tension FEM à la borne du moteur est nulle au repos ou vitesse nulle) qui génère un couple moteur important (on sait que le couple est proportionnel au courant). Mais une fois le moteur est mis en mouvement, le courant revient au régime permanant. Pour information, le courant au démarrage peut atteindre 10 fois le courant dans le régime permanant !

Après le régime transitoire du moteur, il suffit d’une faible puissance pour entretenir le mouvement. En effet, au départ, la puissance doit combattre toute l’inertie du système ; alors qu’en régime continu il n’y a plus qu’à compenser l’élément dissipatif dû généralement aux frottements.

Comment calculer la puissance électrique ?

La puissance électrique que l’on note souvent P et qui a pour unité le watt (symbole W) est le produit de la tension électrique U aux bornes de laquelle est branché l’appareil (en volts) et de l’intensité du courant électrique I qui le traverse (en ampères) pour des appareils purement résistifs. En régime continu la puissance est définit par l’équation suivante :

P=U*I

L’unité de puissance du SI est le watt (symbole : W), qui correspond à un joule fourni par seconde.

Note : On utilise le cheval pour les moteurs thermiques : 1 ch = 736 W environ.

C’est quoi la puissance instantanée ?

Si la tension v(t)ou le courant i(t) varient, la puissance instantanée p(t) consommée par une charge à curant continu est égale au produit des valeurs instantanées du courant qui le traverse et de la tension à ses bornes :

P(t)=u(t)*i(t)

La puissance instantanée est utile lorsque on s’intéresse à l’étude et l’analyse transitoire du courant au borne de la charge (Exemple : le PIC du courant au démarrage, l’allure du courant au moment de changement du rapport cyclique par un signal PWM (Ex : Passage du 60% à 70%), etc.).

C’est quoi la puissance moyenne ?

La puissance moyenne P est l’intégration de la puissance instantanée p(t) dans une période donnée T divisée par la période T.

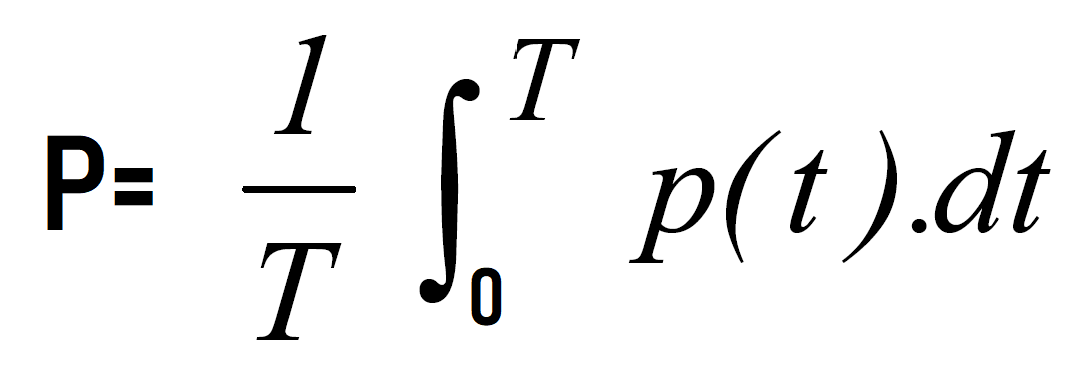
La puissance moyenne est équivalente à un filtre passe bas de la puissance instantanée. La puissance moyenne (effet d’intégration) a la particularité d’être stable par rapport à la puissance instantanée : La valeur change lentement en fonction de la période d’intégration, la puissance est mis à jour chaque période intégration (Ex : 1s, 10s ou un minute en fonction de l’application visée). Elle est pratique comme indicateur de mesure de puissance.

Inconvénient majeur : On ne peut pas observer les phénomènes transitoires de la puissance (Ex : PIC au démarrage, surcharge, surintensité, etc.) car ils sont filtrés par l’intégration.

Dans notre projet on va s’intéresser à la mesure de la puissance instantanée et la puissance moyenne à la borne d’une charge (moteur à courant continu).

Comment mesurer la puissance d’une charge ?

C’est très bien de savoir comment faire le calcul théorique des puissances, mais il faut aussi savoir l’implémenter dans un microcontrôleur. Pour une charge DC (à courant continu), il faut deux grandeurs i (t) et v(t)pour la mesure de la puissance. La mesure de la tension est relativement simple à la borne d’une charge par rapport à la mesure du courant. La plupart des µC disposent des entrées analogiques de tensions mais peut d’entre eux disposent d’une entrée analogique du courant. Dans notre cas on va utiliser un Arduino mini, il est dédié de 8 entrées analogiques sur 10 bits avec une résolution de 4.8 mV (4.8E-3 = 5/1023) (valeur minimale de tension qu’on peut lire avec une entrée analogique).Ci-dessous quelques techniques de mesures du courant :

Dans la pratique, la mesure de courant est très largement utilisée. Le but de cet article est d’étudier sommairement les principales méthodes utilisées en fonction des exigences imposées par l’environnement, principalement

• niveau de courant à mesurer
• précision, résolution, stabilité
• avec ou sans séparation galvanique
• réponse en fréquence (AC/DC)
• environnements (température, durée de vie…)

Dans le choix de l’instrumentation de mesure, les coûts du matériel et de son utilisation sont de première importance. Il est donc nécessaire d’optimiser le design de manière à répondre aux maximums des exigences du cahier des charges. Les techniques de mesure couramment

• Shunt de mesure
• Transformateur de courant
• Capteur de courant basé sur la mesure directe d’induction
• Transducteur de courant sans circuit magnétique (bobine de Rogowski)
• Capteur de courant à effet Hall
• Capteur à champ moyen nul de type Fluxgate
• Capteur de courant basé sur l’effet Néel

A- Capteur de courant avec bobine de Rogowski: 

Très utilisé pour la mesure AC du courant (courant alternatif) en utilisant l’effet Hall. Pour les mesures de courants alternatifs (AC), c’est à dire sans composante continue (DC) une bobine placée dans l’air et magnétiquement couplée avec le conducteur primaire. Il ne s’agit ni plus ni moins que d’un transformateur à faible couplage. Le bobinage est réalisé de manière à avoir une surface maximum offerte au champ d’induction magnétique produit par la circulation de courant dans le conducteur principal (enroulement primaire) mais une surface aussi petite que possible aux champs parasites externes.

• Capteur de courant

B- Mesure du courant avec un Shunt

Elle consiste l’utilisation d’une résistance spéciale (Shunt) pour la mesure du courant en utilisant la loi d’Ohm. En effet lorsque une résistance de valeur R (connue) est parcourut par un courant i(t), la tension au borne de la résistance est égale à u(t)=R*i(t). Ensuite il suffit de lire la tension v(t)à la borne de la résistance avec un µC pour en déduire le courant i(t)=u(t)/R.

Caractéristiques principales du Shunt :

• Courant maximale
• Tension  maximale
• Valeur de la résistance
• Puissance
• Linéarité : Montre comment la tension à la borne de la résistance variée en fonction du courant. U=RI pour une erreur de linéarité =0%.
• Précision : A quel point  la valeur est précise. Exemple: Pour une précision de 5% d’une résistance d’1 Ohm, la valeur mesurée peut variée entre 1+0.05 et 1-0.05. La précision est importante, elle influence également l’erreur sur la tension au borne de la résistance pour un courant donnée.

Exemple : On cherche à mesurer un courant I=10A à la borne d’une charge, R=1 (5%). Alors la tension acquise par le µC peut variée entre 10.5V et 9.5 qui correspondent à une erreur de tension d’1V  ou 1A (erreur du courant)!

• Exemple Datasheet Shunt HS I
• Exemple Datasheet Shunt HS II

Comment brancher un shunt de courant ?

L’objectif d’un shunt est la mesure du courant parcourut par une charge, donc il faut que le shunt soit branché en série avec la charge. Question : est ce que la position du shunt (en aval ou en amant par rapport à la charge) a d’effet sur la mesure?

On considère une charge alimentée par une tension v(t) et parcourue par un courant i(t) (voir la figure ci-dessous). La tension à la borne de la charge est égale à Vch(t). Vsh(t) est la tension à la borne du shunt de résistance =R. On a :

V(t) = Vsh(t)+Vch(t) avec Vsh(t)=R*i(t)

Montage en amont (A):

• La tension Vsh(-) est branchée avec la masse c.à.d. la tension Vsh(-) est environ égale à 0V, par conséquent Vsh(t)=Vsh(+)
• La mesure de la tension à la borne du Shunt peut être effectuée par un simple µC avec une seule entrée analogique Vsh(+) (car l’entrée Vsh(-) est nulle). Dans ce cas on n’a pas besoin d’une mesure différentielle de la tension à la borne du Shunt.
• La valeur de la tension Vsh(t)=Vsh(+) est très faible, elle dépend uniquement de la résistance R et le courant parcouru par la charge. Exemple : Pour R=0.01 et I=100A => Vsh(+)=R*I=1V.

Montage en aval (B):

• L’entrée Vsh(+) est liée avec l’alimentation principale de la charge : Vsh(+)=v(+) !! Par exemple si la charge est alimentée avec une tension de 12V => Vsh(+)=12. Dans ce mode du montage il faut etre sure que l’entrée analogique de µC peut supporter la tension Vsh(+). Dans notre cas on ne doit pas dépasser une tension de l’ordre de 5V.
• La mesure de la tension à la borne du Shunt doit être effectuée d’une façon différentielle : Vsh(t)=Vsh(+)-Vsh(-)=R*i(t) car la tension Vsh(-) est non nulle, elle est égale à la tension à la borne de la charge Vch(+). Dans ce cas il faut un amplificateur d’instrumentation pour la mesure de la tension différentielle Vsh(t). Nommions, on peut utiliser deux entrées analogiques A0 et A1 par exemple pour l’acquisition des tensions Vsh(+) et Vsh(-) successivement ensuite en déduire la tension différentielle Vsh(t)=Vsh(+)-Vsh(-) d’une façon logicielle. Cette technique est peut efficace, mais les résultats sont satisfaisantes.
• En résumé ce montage est risqué car il dépend également de la tension d’alimentation de la charge. Si pas exemple on cherche à calculer la puissance à la borne d’un moteur à CC 12V, ce type de montage sera pas possible car les entrées analogiques de l’Arduino ne peuvent pas supportées une tension au delà de 5V même si la tension différentielle R*i(t)=Vsh(+)-Vsh(-) est de l’ordre de mV ! Parce qu’avant de calculer la différence, on doit d’abord mesurer les deux tensions d’une façon séquentielle (des entrées positive et négative).

On peut utiliser une mesure différentielle du courant pour plus de précision du montage (A)

Comment calculer la valeur moyenne d’un signal numérique ?

La valeur moyenne d’un signal numérique s(n) de taille N échantillons est égale à la somme des échantillons s(i) (pour i varié de 1 à N) divisé par N. En électronique la valeur moyenne est équivalente à la composante continue du signal. Ci-dessous la formule de la base de la moyenne  d’un signal numérique X(n):

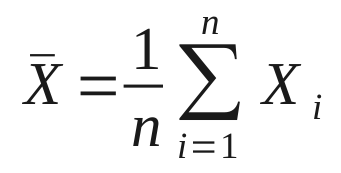
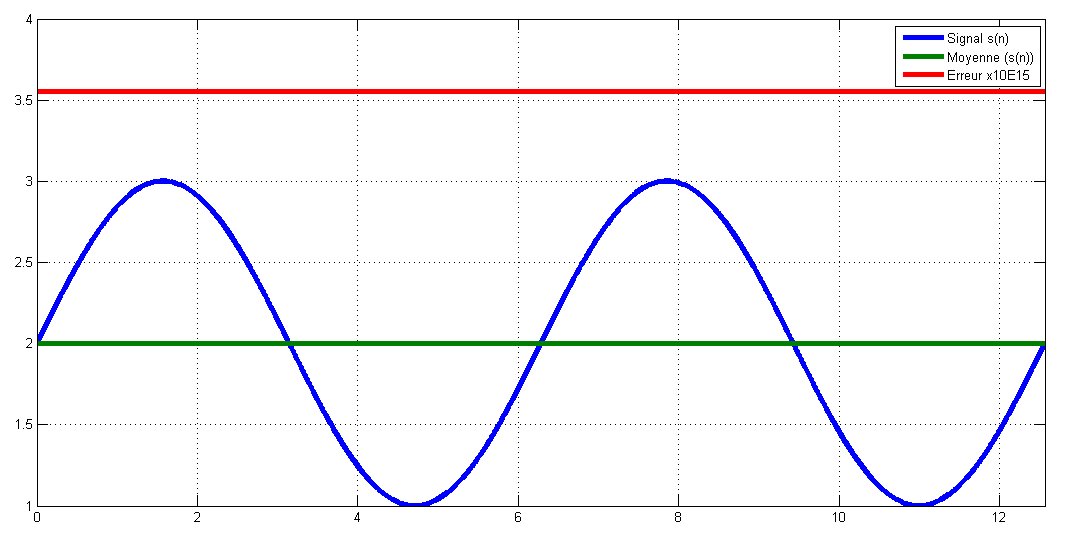
Exemple I: Calcule de la valeur moyenne d’un signal sinusoïdal d’amplitude 1 avec un composante continue égale à 2. le programme ci-dessous illustre comment retrouver la composante DC du signal en utilisant la formule de la moyenne et l’erreur correspondante. Ici l’erreur entre la valeur théorique et la valeur calculée de la composante DC est de l’ordre de 10^-15.

clear all; close all; clc;

% Signal
N=1e4;
moy_theo=2;
amp=1;
t=linspace(0,4*pi,N);
s_n=amp*sin(t)+moy_theo;

% Calcul de la moyenne
Moy_cal=0;
for i=1:N
    Moy_cal=Moy_cal+s_n(i);
end
Moy_cal=Moy_cal/N;
Moy_sig=Moy_cal*ones(1,N);

% Erreur
Err=moy_theo-Moy_cal
Err=1e15*Err*ones(1, N);

% Affichage
h=plot(t,s_n,t,Moy_sig,t,Err , 'LineWidth',4); grid on;
xlim([t(1) t(end)])
legend('Signal s(n)','Moyenne (s(n))','Erreur x10E15');

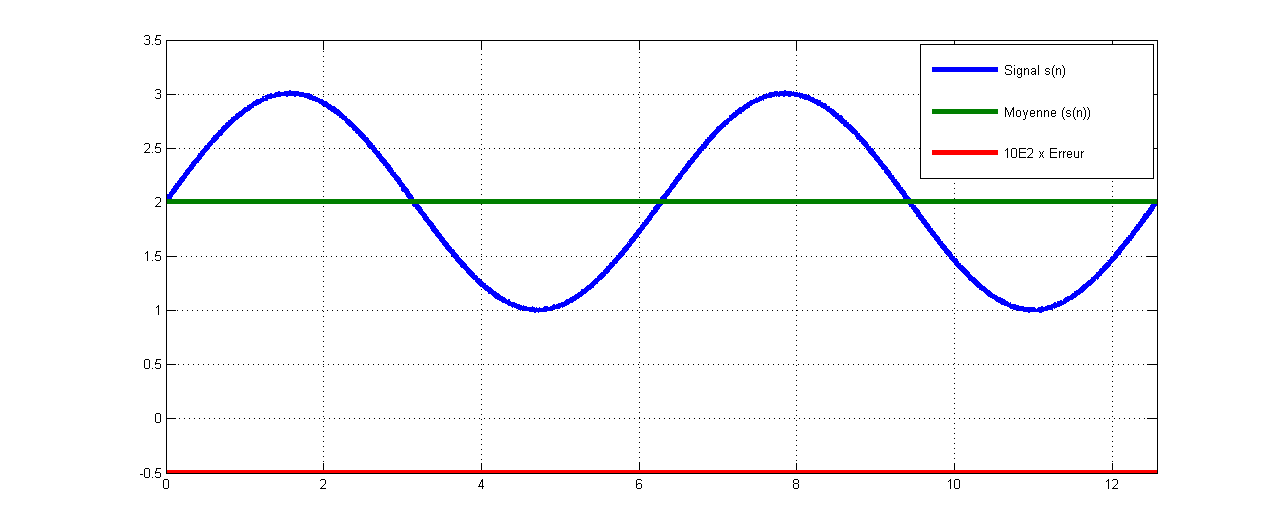
Exemple II: Signal +Bruit ==> Erreur importante de l’ordre de 10^-2

clear all; close all; clc;

% Signal
N=1e4;
moy_theo=2;
amp=1;
t=linspace(0,4*pi,N);
s_n=amp*sin(t)+moy_theo;

% Bruit
s_b=1e-2*rand(1, N);

% Signal + Bruit
s_n=s_n+s_b;

% Calcul de la moyenne
Moy_cal=0;
for i=1:N
    Moy_cal=Moy_cal+s_n(i);
end
Moy_cal=Moy_cal/N;
Moy_sig=Moy_cal*ones(1,N);

% Erreur
Err=moy_theo-Moy_cal
Err=1e2*Err*ones(1, N);

% Affichage
h=plot(t,s_n,t,Moy_sig,t,Err , 'LineWidth',4); grid on;
xlim([t(1) t(end)])
legend('Signal s(n)','Moyenne (s(n))','10E2 x Erreur');

Implémentation sur Arduino de calcule de la moyenne

A- calcul par bloc de la moyenne : On considère un tableau Tab de taille 8 (8 valeurs) initialisé à 0. La moyenne par bloc consiste la mise à jour des 8 valeurs du tableau  via 8 lectures d’une entrée analogique de l’Arduino. L’étape suivante consiste le calcul de la valeur moyenne. Ci-dessous un extrais du code de la méthode :

Exemple :

1. Initialisation : Tab[8]={0,0,0,0,0,0,0,0}
2. Remplissage du tableau (8 opérations de lecture) Tab[i] :lecture de l’entrée analogique (A0, A1,…)
3. Calcule de la valeur moyenne du tableau : Moy=(Tab[0]+ Tab[1]+.. +Tab[7])/8

Inconvénients de la méthode :

1. Nécessite N lectures/ calcule de la valeur moyenne (Inefficace lorsque N devient important : N=128,256,…)
2. Perte des échantillons précédents du tableau : On écrase toutes les valeurs pour chaque opération de calcul de la moyenne

B- Calcul en utilisant la moyenne glissante : La méthode consiste la mise à jour d’une seule case du tableau pour chaque itération sans pertes des échantillons précédents. Autrement dit, une seule lecture de l’entrée analogique par itération. La méthode permet d’obtenir la valeur moyenne par chaque itération ! La technique est beaucoup plus rapide par rapport à la téchnique précédente, elle nécessite une seule lecture/ itération et indépendant de la taille du tableau. Ci-dessous les étapes principales des de la méthode. On considère un tableau Tab de taille 8 initialisé à 0.

• Lecture 1 : Tab[0] : lecture de l’entrée analogique & Moy= (Tab[0]+0+0+0..+0)/8
• 2. Lecture 2 : Tab[1] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+0+0..+0)/8
• 3. Lecture 3 :   Tab[2] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+ Tab[2]+0..+0)/8
• 4. Lecture 4 : Tab[3] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+ Tab[2]+ Tab[3]..+0)/8
• …
• 8. Lecture 8 : Tab[7] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+ Tab[2]+ Tab[3]+ Tab[4]+ Tab[5]+ Tab[6]+ Tab[8])/8
• 9. Lecture 9 : Tab[0] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+ Tab[2]+ Tab[3]+ Tab[4]+ Tab[5]+ Tab[6]+ Tab[8])/8
• 10. Lecture 10 : Tab[1] : lecture de l’entrée analogique & Moy= (Tab[0]+ Tab[1]+ Tab[2]+ Tab[3]+ Tab[4]+ Tab[5]+ Tab[6]+ Tab[8])/8
• …

Inconvénient unique de la méthode :

Le temps de réponse de la moyenne est égal à N-1 itérations : Il faut N itérations avant que le tableau soit complètement remplis. On peut observer ce dernier dans le régime transitoire de la moyenne. Ci-dessous un exemple matlab illustrant le principe de la méthode :

Programme de calcul de la valeur moyenne

clear all; close all; clc;

% Signal
num_itte=1e4;
moy_theo=2;
amp=1;
t=linspace(0,100*pi,num_itte);
s_n=amp*sin(t)+moy_theo;

% Bruit
s_b=1e-1*rand(1, num_itte);

% Signal + Bruit
s_n=s_n+s_b;

% Calcul de la moyenne glissante
Moy_gliss=zeros(1,num_itte);
% Taille=256;
% Taille=512;
% Taille=1024;
Taille=2048;

j=1;
Tab=zeros(1,Taille);
for i=1:num_itte
    % Cacul de  la moyenne
    Tab(j)=s_n(i);
    Moy_gliss(i)= mean(Tab); % Moyenne Tab

    % Mise à jour de l'indice
    j=j+1;
    j=mod(j,Taille);
    if j==0
        j=1;
    end
end

% Calcul de l'erreur
Err=moy_theo-Moy_gliss;

% Affichage
subplot(211);
h=plot(t,s_n,t,Moy_gliss, 'LineWidth',2); grid on;
xlim([1 t(end)])
legend('Signal s(n)','Moyenne (s(n))');
title('N=2048');

subplot(212);
h=plot(t,Err, 'LineWidth',2); grid on;
xlim([t(1) t(end)])
legend('Erreur');
title('N=2048');

Simulation pour N=256

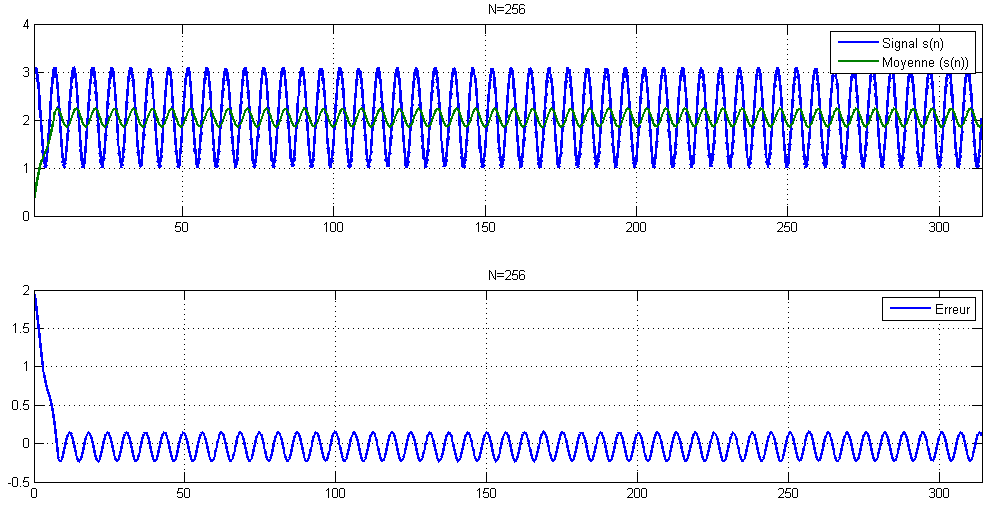
Simulation pour N=512

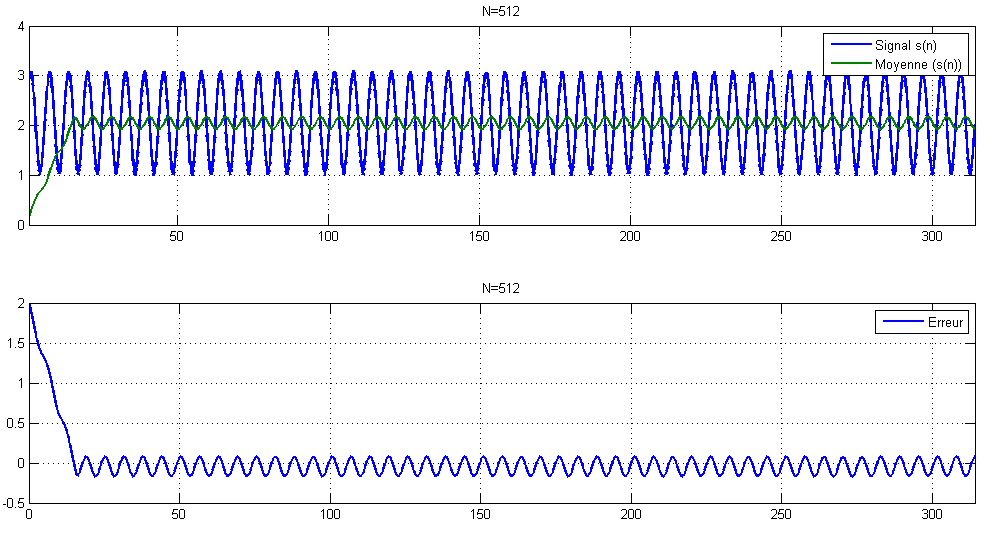
Simulation pour N=1024

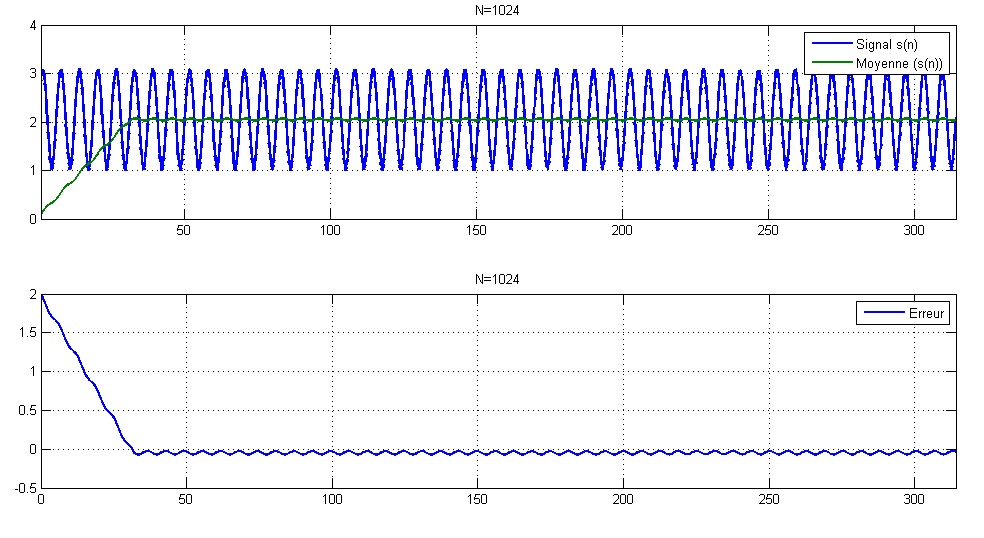
Simulation pour N=2048

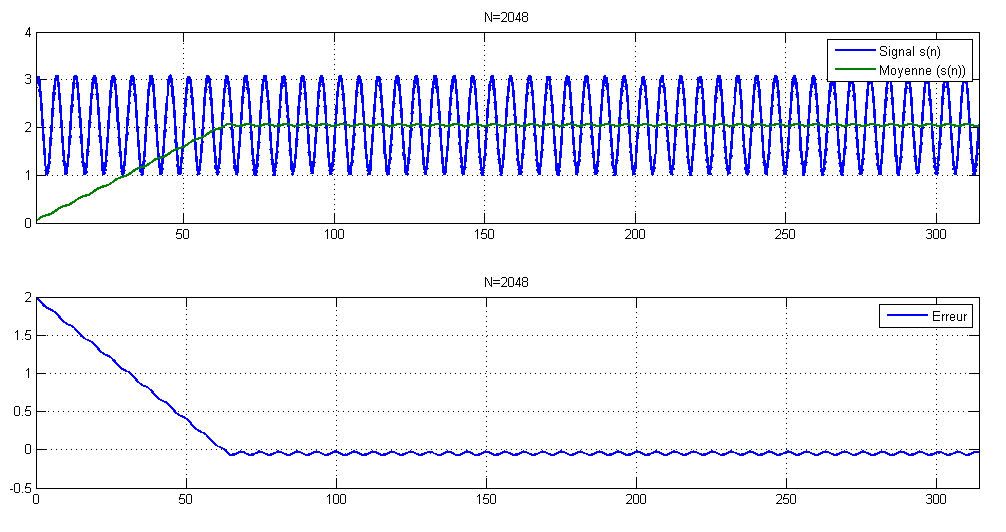
Montage Arduino

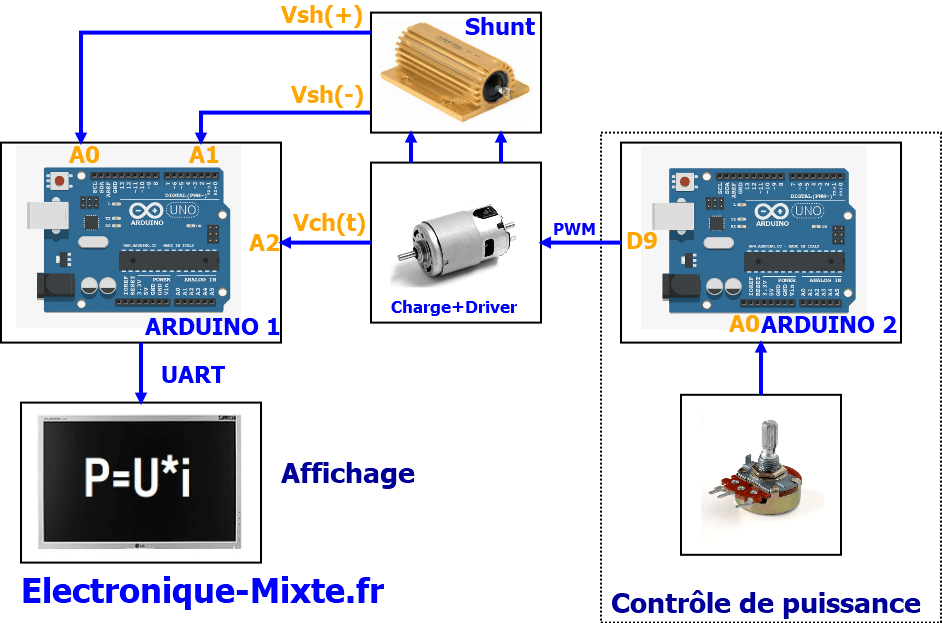
Programme Arduino 1:

// Paramètres du courant
int Courant_pin_P = A0;
int Courant_pin_N = A1;
int Val_I=0;
float courant_val_P=0.0;
float courant_val_N=0.0;
float courant_val=0.0;
float Val_shunt_R=2.7; // shunt du courant en Ohm

// Paramètres de la tension
int Volt_pin = A2;
int Val_A2=0;
float volt_val=0.0;

// Puissance
float Puissance_inst_mW=0.0;
float Pissance_moy_mW=0.0;

// All
const float Max_volt=5.0;
const float Max_ADC=1023; // 2^10 - 1
const unsigned char TailleMoy=4;
const unsigned char TailleTab=4;
unsigned char ValIndex=0;
float DataIn[TailleTab];

void setup()
{
        // Seria port
        Serial.begin(9600);
}
void loop() {

        // Mesure du courant
        Val_I = analogRead(Courant_pin_P);delay(100);
        courant_val_P=float(Val_I)*Max_volt/Max_ADC; // +

        Val_I = analogRead(Courant_pin_N);delay(100);
        courant_val_N=float(Val_I)*Max_volt/Max_ADC; // -

        courant_val=abs(courant_val_P-courant_val_N)/Val_shunt_R; // Valeur en Ampère

        // Mesure de la tension
        Val_A2 = analogRead(Volt_pin);
        volt_val=float(Val_A2)*Max_volt/Max_ADC;
        //volt_val=5.0;

        // Calcul de la puissance instantannee
        Puissance_inst_mW=courant_val*volt_val;
        Puissance_inst_mW=Puissance_inst_mW*1000.0;

        // Cacul de la puissance moyenne
        TabSet(TailleTab,  ValIndex, DataIn, Puissance_inst_mW);
        Pissance_moy_mW=Moyenne(TailleTab, TailleTab,  DataIn);

        //Affichage I/V
        Serial.print("\n Courant(mA):");
        Serial.print(1000*courant_val);
        Serial.print("\n Tension(V):");
        Serial.print(volt_val);

        //Affichage des puissances
        Serial.print("\n Puissance Inst(mW):");
        Serial.print(Puissance_inst_mW);
        Serial.print("\n Puissance Moy(mW):");
        Serial.print(Pissance_moy_mW);
        Serial.print("\n");

        // Mise à jour indice
        ValIndex=ValIndex+1;
        if (ValIndex==TailleTab)
        {
            ValIndex=0;
        }

        // Délai
        delay(800);
}

float Moyenne(unsigned char NumMean,unsigned char Taille,  float *DataIn)
{
        int i=0;
        float somme =0.0;
        for(i=0;i<NumMean; i++)
                somme+=DataIn[i];

        return somme/NumMean;
}

void TabSet(unsigned char Taille, unsigned char ValIndexTmp, float *DataIn, float ValPowIst)
{
  DataIn[ValIndexTmp]=ValPowIst;
}

Programme Arduino 2

// ARDUINO 2: Contrrole de puissance

// Sortie PWM
int To_Moteur_PWM = 9;

// Entree potentiometre
const int Potent_pin = A0;
int val_Pot = 0;

void setup()
{
    // Sortie PWM
    pinMode(To_Moteur_PWM, OUTPUT);

    // Seria port
    Serial.begin(9600);
}
void loop() {

      //Lecture Poto
      val_Pot = analogRead(Potent_pin);

     // Génération du signal PWM
     analogWrite(To_Moteur_PWM, val_Pot/4);
     analogWrite(10, val_Pot/4);

     // Affichage
     Serial.print(val_Pot/4);
     Serial.print("\n");

     // Délai
     delay(1000);
}

Effet du rapport cyclique (0(0%) et 255 (100%)) sur  la tension à la borne du moteur à courant continu

La courbe en jaune montre la tension PWM à vide (sortie Arduino en air), la courbe bleue montre la tension à la borne du moteur. En bas des courbes l’interface série illustrant le rapport cyclique correspondant (voir les images ci-dessous):

[masterslider id= »9″]

Photos du projet

[masterslider id= »10″]

************

Un petit commentaire de vous, un Grand encouragement pour nous ?

************

Téléchargement du projet

************