Découvrez notre Chaîne YouTube "Ingénierie et Projets"
Découvrez notre Chaîne Secondaire "Information Neuronale et l'Ingénierie du Cerveau"
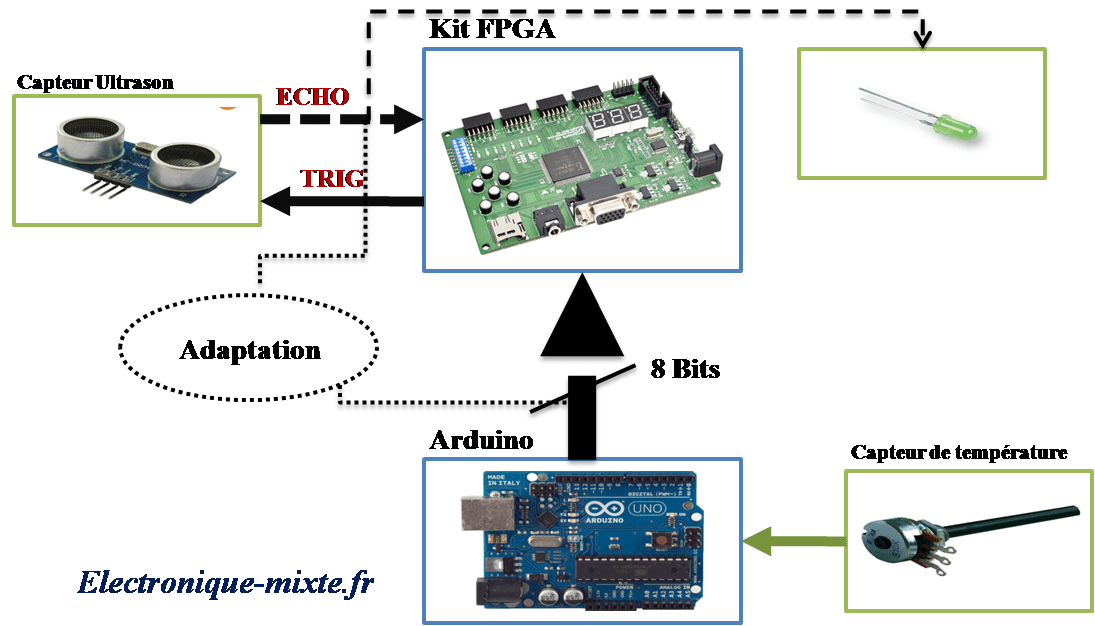
Les objectifs du projet
- Se familiariser avec le codage en virgule fixe
- Choix de la position de la virgule (précision)
- Choix de nombre des bits
- Opérations sur les données en virgule fixe
- Implémentation d’une équation en virgule fixe
- Savoir la relation entre la distance, température pour un capteur ultrasonique
Le codage en virgule Fixe
En informatique, une représentation d’un nombre en virgule fixe est un type de donnée correspondant à un nombre qui possède (en base deux ou en base dix) un nombre fixe de chiffres après la virgule. Les nombres en virgule fixe sont utiles pour représenter des quantités fractionnaires dans un format utilisant le complément à deux quand le processeur de l’ordinateur n’a aucune unité de calcul en virgule flottante ou quand une virgule fixe permet d’augmenter la vitesse d’exécution ou d’améliorer l’exactitude des calculs. La plupart des processeurs à faible coût (ex. : microcontrôleurs) ne disposent pas d’unité de calcul en virgule flottante.
Les bits à gauche de la virgule représentent la partie entière du nombre (au sens premier du terme), c’est-à-dire l’entier se trouvant à gauche de la virgule. Chaque bit à droite de la virgule, ou « décimale binaire », correspond à l’inverse d’une puissance de 2 [wikipedia].
Présentation d’un nombre en virgule fixe en format Qn
n : le nombre des bits nécessaires pour le codage de la partie fractionnelle
m : le nombre des bits nécessaires pour le codage de la partie entière
Voir les liens des cours en bas pour plus des renseignements.
Règles de l’arithmétique en virgule fixe :
Calcul de la résolution binaire en fonction de la résolution décimale
On considère D la résolution décimale d’un nombre décimal (Ex : 10-3 pour D=3) et n la résolution binaire d’un nombre binaire (Ex : 2-3 pour n=3)
Exemple
x = 10.12
x = 10 + 0.12 = xm + xn
Codage de 10 (xm) : 10 = (1100)2, m=4 bits
Codage de 0.12 (xn) : D’après la relation ci-dessus 0.12*102=12 (valeur entière, D=2)
On prend alors n>=3.32*2 = 6.64 = 7 bits, n=7 bits
Xn = Round (0.12*2^7) =Round (15.36) =15 = (0001101)2
La présentation binaire du nombre x= 10.12 sous le format Q7 sur 10 bits est la suivante :
X = 1100,0001101
Alors la largeur non signé de la donnée doit être codée sur 4+7 = 11 bits ou 12 bits pour un nombre signé, la position de la virgule se trouve entre le bit 7 et le bit 8 (virgule virtuelle)
Cours : IRISA & IUT REIMS & ENS LYON
La distance en fonction de la température
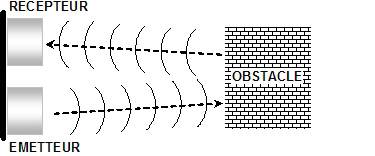
la vitesse du son dans l’air augmente quand la température augmente. Cair = (331,5 + 0,6·Temp) ; Temp température en Celcius
Cair = (331,5 + 0,6·Temp)
La distance entre l’émetteur et le récepteur d est égale à V*t/2, avec V la vitesse de propagation de l’onde dans l’air et t le temps du trajet aller/Retour entre l’emetteur et le recepteur. Alors :
d = V*t/2 = Cair *t/2= t*(331,5 + 0,6*Temp)/2
d(m) = t*(165.75 + 0,3*Temp)
d(m) = (N*t0)*(165.75 + 0,3*Temp)
d(m) = N*(165.75 + 0,3*Temp)*83.3333.10-9
d(m) = N*(13.8125+ 0.025*Temp)*10-6
d(mm) = N*(13.8125*10-3+ 0.025*10-3*Temp)
d(mm)=N*(K0 + K1*Temp)
- t0=1/f0=83.33ns pour f0=12 MHz
- N le valeur du compteur sur 24 bits
- Temp température entre 0° et 100° sur 8 bits
- K0 = 13.8125*10-3
- K1 = 0.025*10-3
Codage en virgule fixe des constantes K0 et K1
- K0 =13.8125*10-3 = 0.0138124
La partie entière est codée sur 0 bits. On respectant la formule nk0 = D*3.322 on obtient (pour D=3) n = 3*3.322 = 9.966. On prend nk0=10 bits
(k0)2= Round(k0*210)=(14)2 = (.0000001110)2
- K1=0.025*10-3=25*10-5
La partie entière est codée sur 0 bits. On respectant la formule nk1= D*3.322 on obtient (pour D=5) n = 5*3.322 =16.61. On prend nk0=17 bits
(k1)2= Round(k1*217)=Round(32.768) = (33)2 = (.00000000000100001)2
Remarque : Tous les bits des constanctes k0 et K1 sont consacrés à la partie fractionnelle (0<k0<1 et 0<k1<1)
- K0(m,n) = (0,10), la longeur de la constante K0 est égale à m+n = 10 bits, format en virgule fixe (voir la séction ci-dessus)
- K1(m,n) = (0,17), la longeur de la constante K1 est égale à m+n = 17 bits
Codage de la valeur de la température
La température Temp est codé sur 8 bits, la valeur de la température variée entre 0°C et 100 °C. Afin de convertir la valeur binaire en température il suffit d’appliquer la règle de trois ! 0 pour 0 °C et 255 (8 bits) pour 100 °C.
Temp(°C) = Temp * 100/255
Temp(°C) = Temp * 0.3922
Temp(°C) = Temp2 * Ktemp
== > d(mm)=N*(K0 + K1*Temp2 * Ktemp) (1)
- Ktemp=0.3922 =39.22*10-2
La partie entière est codée sur 0 bits. On respectant la formule nktemp= D*3.322 on obtient (pour D=2) n =2*3.322 =6.64. On prend ntemp=7 bits
(ktemp)2= Round(ktemp*27)=Round(50.2016) = (50)2 = (.0110010)2
Conclucion
Codage des variables et constantes sur le format Q(m,n) avec n le nombre des bits de la partie entière, et m le nombre des bits de la partie fractionnelle. m+n est le nombre des bits total de la variable.
-
Temp2 : (8,0), Taille 8 bits [8+0]
-
Ktemp : (0,7), Taille 7 bits
-
K0 : (0,10), Taille 10 bits
-
K1 : (0,17), Taille 17 bits
-
N : (24,0), Taille 24 bits
-
Kt : (0,20) (voir la formule 2), Taille 20 bits
On peut simplifie la formule (1) de la distance on remplaçant Ktemp*K1 par Kt = Ktemp*K1
d(mm)=N*(K0 + Temp2 * Kt) (2)
- Kt=Ktemp*K1 = (100/255)*0.025*10-3 =9.8*10-6
La partie entière est codée sur 0 bits. On respectant la formule nkt= D*3.322 on obtient (pour D=6) n =6*3.322 =19.9. On prend nkt=20 bits
(kt)2= Round(kt*220)=Round(10.27) = (10)2 = (.00000000000000001010)2
Pour optimiser la longueur de Kt, on peut intégrer la fonction Ktemp sur l’Arduino, au lieu de transmettre la valeur brut sur 8 bits, on transmit la valeur de la température [0-100] (après multiplicateur par 100/255 et arrondi de la valeur finale).
1 commentaire
Projet électronique #17: Sèche-mains ultrason avec Arduino – FPGA | Arduino | Matlab | Cours · 2018-10-09 à 5:37
[…] PROJET ÉLECTRONIQUE FPGA 4 #3/ 3 CAPTEUR DE DISTANCE ULTRASONIQUE À BASE DU FPGA ET ARDUINO – CA… […]