Projet électronique FPGA #7 : Calcul de Factorielle – n!

Rappels de cours:

• Chapitre 6 Les factorielles
• Développements limités usuels en 0
• Calcul Algébrique
• Chapitre 1 identités remarquables
• Les Développements Limités
• Synthèse « Factorielle de n »
• Mathématiques discrètes
• Factorielle et binôme de Newton

Objectifs du projet:

• Comment calculer la factorielle de N ?
• C’est quoi les applications de la factorielle ?
• Comment évaluer la factorielle de N en fonction de N ?
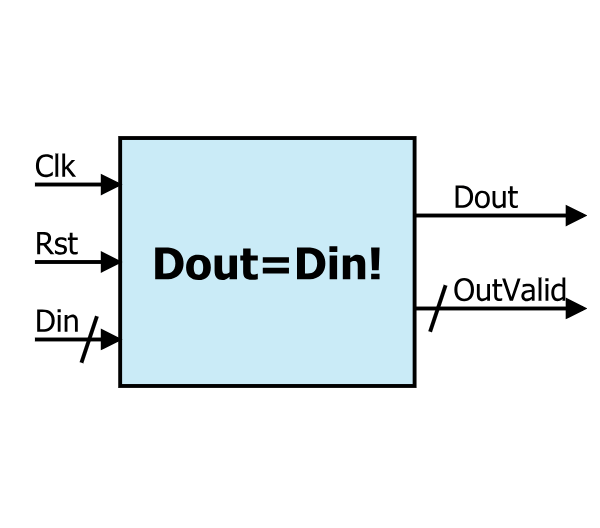
• Comment réaliser un circuit factorielle de N avec VHDL ?
• Comment calculer le nombre des bits de sortie du composant en fonction de N
• Autres astuces pratiques de programmation en VHDL

Définition:

Par définition la factorielle d’un nombre entier N notée N! Strictement positif est le produit des entiers strictement positifs inférieurs ou égaux à N. La formule est donnée par :

N!=n*( N -1)*( N -2)*…..*3*2*1

On peut récrire la formule d’une fonçons récursive comme suit :

N != N *( N -1) ! = N (N -1)( N -2) != N (N -1)( N -2) (N-3) !…

Exemples de calcul de la factorielle de N – N ! :

N   |   N!
---------
00!        1
01!        1
02!        2
03!        6
04!        24
05!        120
06!        720
07!        5040
08!        40320
09!        362880
10!        3628800
11!        39916800
12!        479001600
13!        6227020800
14!        87178291200
15!        1307674368000
16!        20922789888000
17!        355687428096000
18!        6402373705728000
19!        121645100408832000
20!        2432902008176640000
21!        51090942171709440000
22!        1124000727777607680000
23!        25852016738884976640000
24!        620448401733239439360000
25!        15511210043330985984000000
26!        403291461126605635584000000
27!        10888869450418352160768000000
28!        304888344611713860501504000000
29!        8841761993739701954543616000000
30!        265252859812191058636308480000000
31!        8222838654177922817725562880000000
32!        263130836933693530167218012160000000

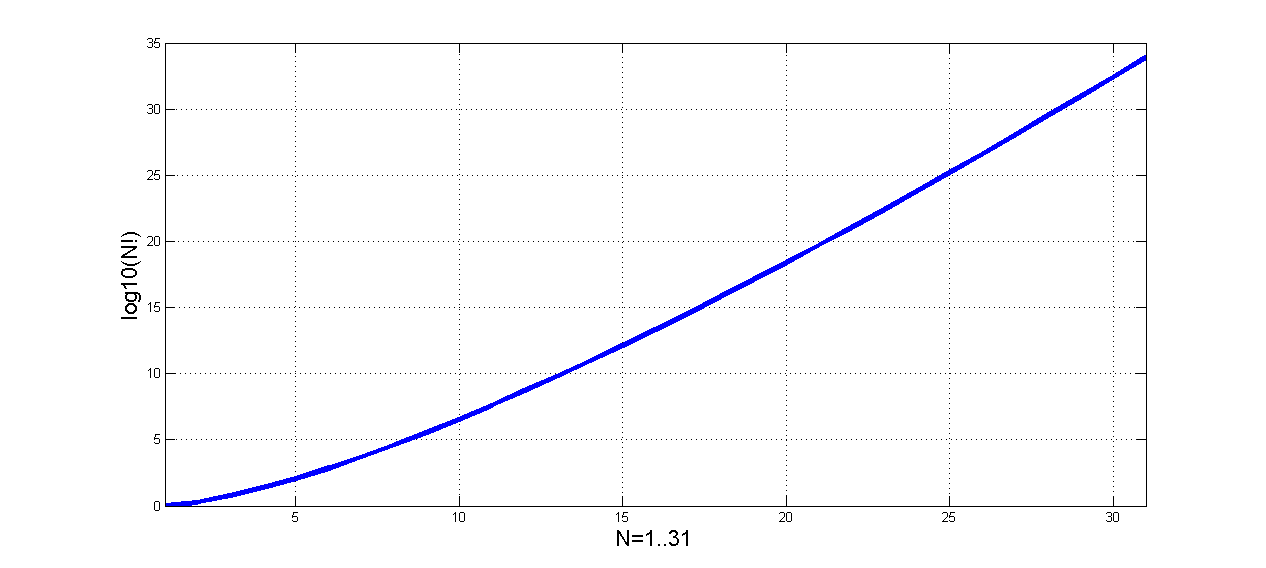
Le nombre des chiffres de la factorielle augmente d’une façon exponentielle avec N. La figure ci-dessous illustre N en fonction du log10(N !). La Coubre montre une croissance linéaire pour N supérieur ou égal à 10. Pour les valeurs inférieures à 10, la factorielle de N reste relativement faible (démarrage lent) en particulier au voisinage de 1.