Objectifs du projet électronique
- Etude et simulation numérique du filtre Moyenneur avec Matlab [1/3]
- Etude et simulation numérique du filtre Médiane avec Matlab [1/3]
- Etudes et simulation numérique des techniques de la détection de seuil [2/3]
- Seuillage classique
- Seuillage moyenné
- Seuillage médiane
- Etude comparatives et qualitative des méthodes [2/3]
- Implémentation sur microcontrôleur en utilisant le kit Arduino [3/3]
Etudes et simulation numérique des techniques de la détection de seuil
Effectuer une mesure, c’est déterminer quantitativement, par un moyen adéquat, la valeur d’une grandeur de nature quelconque (mesurande) et l’exprimer dans une unité appropriée. Le plus souvent, la grandeur à mesurer est traduite en une grandeur électrique. (Extrait du Document d’accompagnement du programme des SI – MEN) Pour que cette grandeur électrique soit facilement exploitable, il est souvent nécessaire de la mettre en forme grâce à une structure de conditionnement. Effectuer une mesure, c’est déterminer quantitativement, par un moyen adéquat, la valeur d’une grandeur de nature quelconque (mesurande) et l’exprimer dans une unité appropriée. Le plus souvent, la grandeur à mesurer est traduite en une grandeur électrique. (Extrait du Document d’accompagnement du programme des SI – MEN) Pour que cette grandeur électrique soit facilement exploitable, il est souvent nécessaire de la mettre en forme grâce à une structure de conditionnement.[Source].
L’objectif de la détection de seuil est de transformer un signal analogique en un signal logique afin de le rendre plus facilement exploitable ou plus facile à traiter.
Exemples d’application :
- Détecteur de niveau
- Détecteur d’un pic de la température
- Limiteur du courant ou de la tension
- Détecteur de présence
- Détecteur d’un objet quelconque
- Détecteur d’un événement ou une longueur d’onde
- Suppression des rebonds
- …
L’objectif principal de ce projet est d’illustrer trois méthodes de base pour la détection d’un seuil. Vous prouvez prendre un coup d’œil sur la première partie du projet pour mieux comprendre la suite de l’article.
1- Technique de seuillage par comparaison
C’est la méthode la plus simple et la moins efficace pour détecter un seuil ! Il consiste a comparé échantillon par échantillon le signal d’entré avec une valeur du seuil fixe, si l’entrée est supérieure ou égale au seuil la sortie vaut ‘1’ sinon la sortie vaut ‘0’. Le principe est identique à un comparateur analogique à base d’un amplificateur opérationnel (voir figure ci-dessous) [Plus des détails].
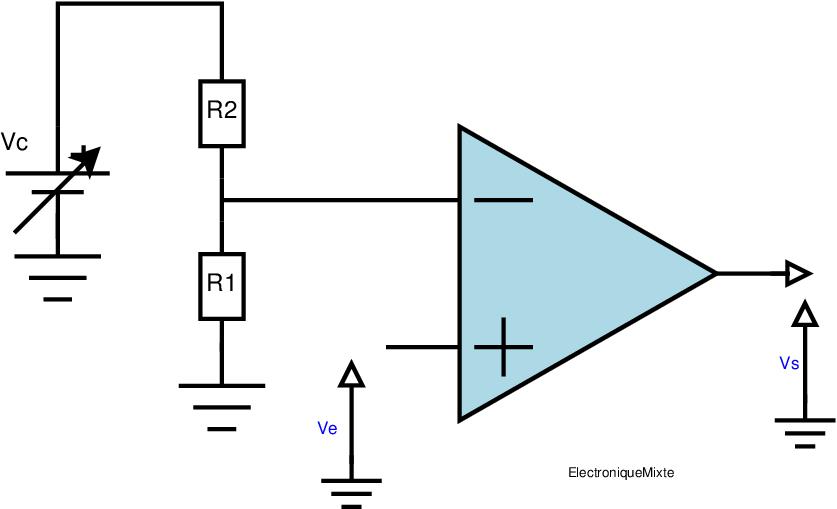
Exemple : R1=R2, Vsat=+/- 15V. Le graphe ci-dessus illustre la tension de sortie pour Vc=2V ,Vc=4V et Vc=16V (Vseuil =1,2 ou 8V)
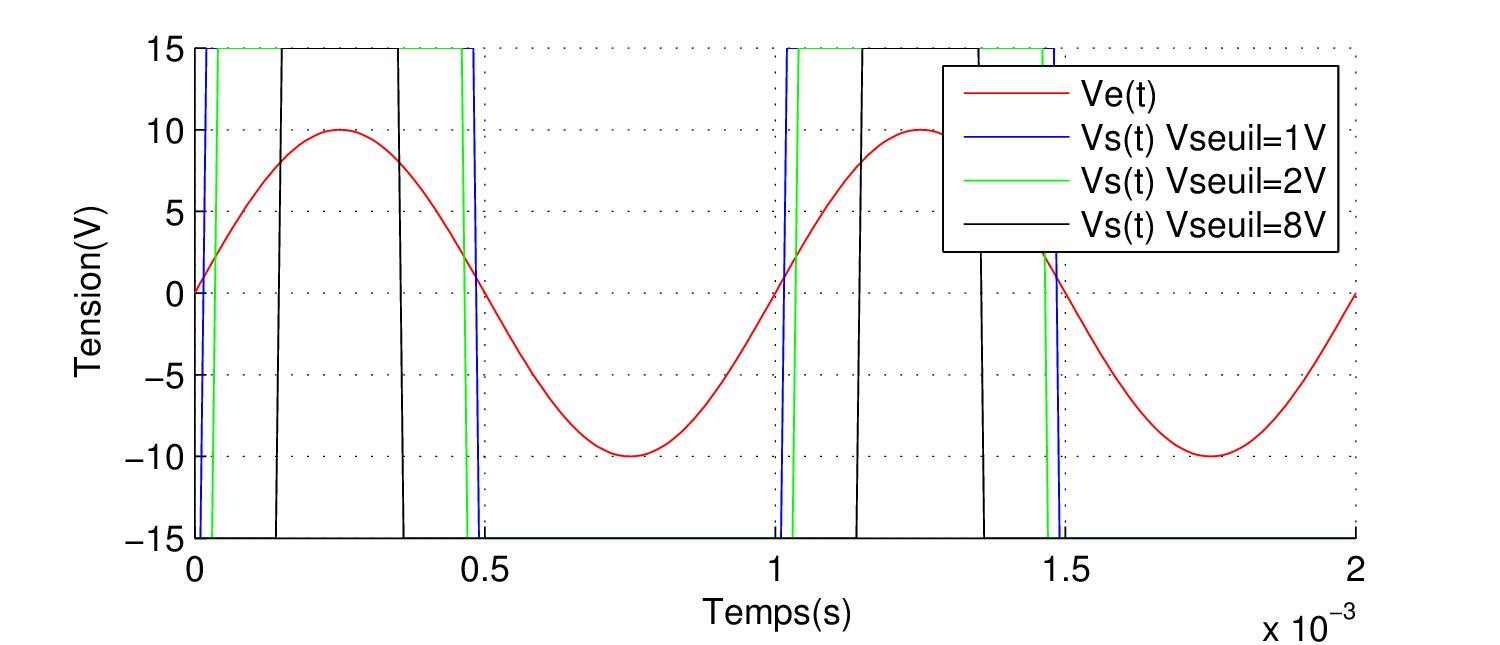
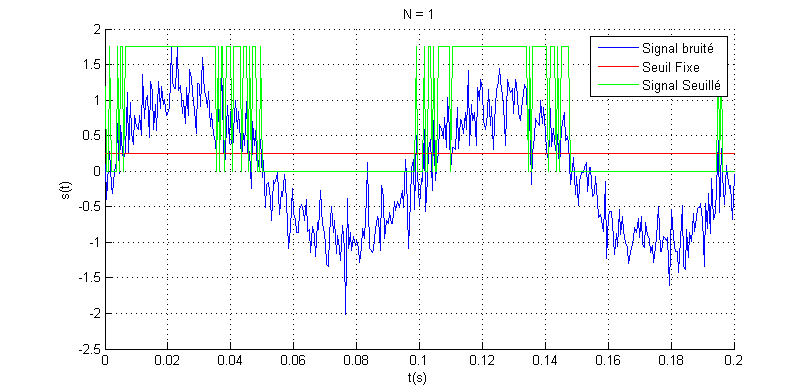
La figure ci-dessus montre la sortie logique pour un seuil fixe avec un signal sinusoïdal parfait à l’entrée, en pratique ce n’est pas toujours le cas 🙁 le signal est généralement additionné avec le bruit interne ou externe su système. La figure ci-dessous montre le signal logique après seuillage pour un signal bruité.
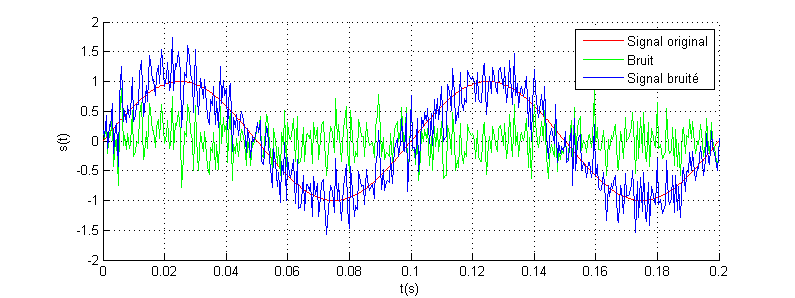
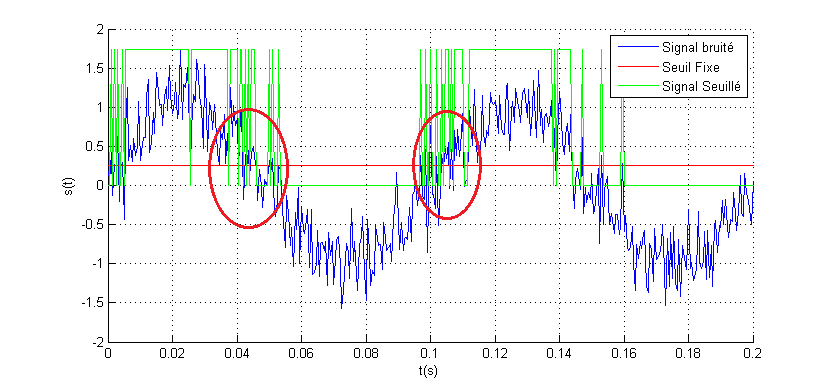
Le bruit du signal analogique est directement transmis au signal logique après l’opération du seuillage (transitions aléatoires au voisinage du seuil). Ce phénomène peut générer des conséquences importantes dans le circuit décisionnel après seuillage. On verra dans la suite du projet, deux techniques de seuillage qui peuvent être utilisées pour illuminer les transirons dues au bruit du signal, on peut les appelées techniques de seuillage filtré 🙂
Programme Matlb
clear all;
close all;
clc;
% Paramètres du signal
F0=10;
T0=1/F0;
Ns=200;
Fs=F0*Ns;
Ts=1/Fs;
% Génération du signal
t= 0:Ts:2*T0;
s_t= sin(2*pi*F0*t);
% Géneration du bruit
Vare = 1e-1;
Mu=0;
b_t = Mu + sqrt(Vare)*randn(1,length(s_t));
% Génération signal + bruit
s_b_t = s_t + b_t;
% Affichage
figure(1);
grid on ; hold on ;
plot(t, s_t,'r');
plot(t,b_t,'g');
plot(t,s_b_t,'b');
legend('Signal original', 'Bruit', 'Signal bruité');
xlabel('t(s)');
ylabel('s(t)');
% 1- Seuillage de base - Seuil fixe
% On prend 1/4 de la valeur maximale du signal comme seuil
Suil = max(s_t)/4;
s_seuil = 0*s_t;
seuil_t=Suil*ones(1,length(s_t));
for i=1:length(s_t)
% Application du seuil
if(s_b_t(i)>=Suil)
s_seuil(i)=1*max(s_b_t);
end
% else
% s_seuil(i)=0;
% end
end
% Affichage
figure(2);
grid on ; hold on ;
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil,'g');
legend('Signal bruité','Seuil Fixe', 'Signal Seuillé');
xlabel('t(s)');
ylabel('s(t)');2- Technique de seuillage moyenné
La technique est basé sur l’utilisation d’un signal filtré ou lissé avant d’appliquer le seuil. Pour comprendre le principe du filtrage moyenné je vous invite de consulter partie 1/3 du projet.
Explication simple de la technique
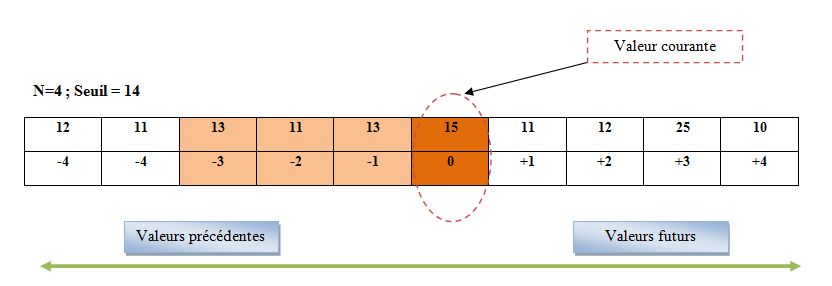

On constate que le résultat logique dépend de N-1 échantillons précédents, donc avant de générer un signal logique il faut faire l’acquisition de N-1 échantillons d’où un retard de N-1 période d’échenillage ! On peut résumer l’algorithme de la technique en trois étapes principales :
- Acquisition de N échantillons ((N-1) échantillons précédents + échantillon actuel)
- Calcul de la valeur moyenne
- Comparaison avec le seuil & Génération de la sortie logique
Les microcontrôleurs ne sont pas adaptés aux opérations du traitement du signal (gestion des buffers et les accès mémoire) en haut débit. Par exemple dans les DSP (Processus du traitement du signal) disposent des buffers circulaires ou linaires à l’entrée ou à la sortie (décalage automatique des échantillons) afin d’éviter la mise à jours du buffer qui contient les échantillons et gagner en temps de traitement. [Cours DSP]
Résultats de simulation avec matlab
Simulation pour N=1 (équivalent au seuillage par comparaison – comparaison échantillon par échantillon)
Simulation pour N varié de 4 à 16
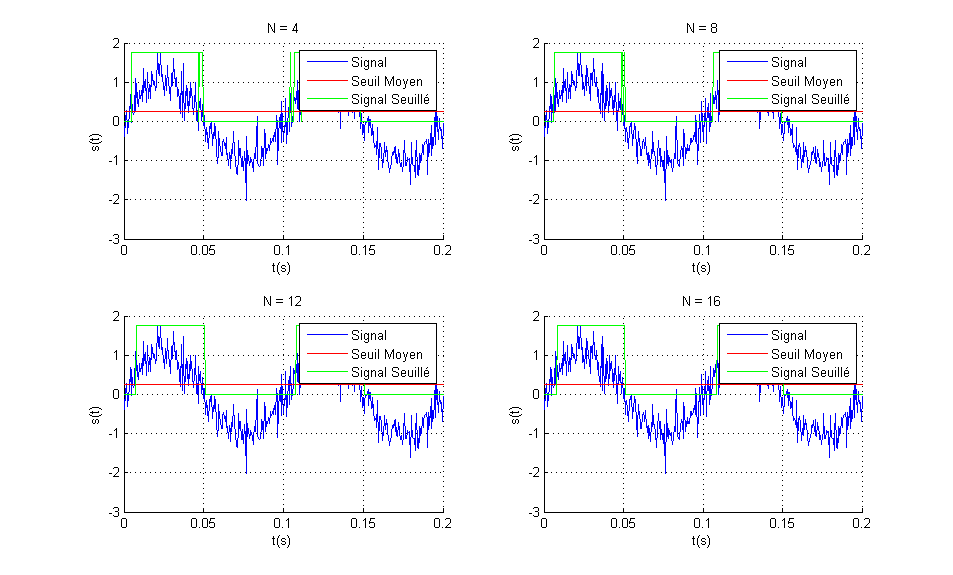
La qualité du seuillage s’améliore avec l’augmentation de la taille du filtre (A partir de N=8).
Programme Matlb
…
% On prend 1/4 de la valeur maximale du signal comme seuil
Suil_mean = max(s_t)/4;
N_seuil_mean=4:4:20;
s_seuil_mean = zeros(length(N_seuil_mean),length(s_t));
seuil_t=Suil_mean*ones(1,length(s_t));
for k=1:length(N_seuil_mean)
for i=N_seuil_mean(k):length(s_t)
% Calcul de la valeur moyenne du signal
Moyenne=mean( s_b_t(i-N_seuil_mean(k)+1:i));
% Application du seuil moyenné
if(Moyenne>=Suil_mean)
s_seuil_mean(k,i)=1*max(s_b_t);
end
% else
% s_seuil(i)=0;
% end
end
end
% Affichage
figure(3);
subplot(221);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_mean(1,:),'g');
legend('Signal','Seuil Moyen', 'Signal Seuillé');
title('N = 4');
subplot(222);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_mean(2,:),'g');
legend('Signal','Seuil Moyen', 'Signal Seuillé');
title('N = 8');
subplot(223);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_mean(3,:),'g');
legend('Signal','Seuil Moyen', 'Signal Seuillé');
title('N = 12');
subplot(224);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_mean(4,:),'g');
legend('Signal','Seuil Moyen', 'Signal Seuillé');
title('N = 16');3- Technique de seuillage médian
La technique est basé sur l’utilisation d’un médian avant d’appliquer le seuil. Pour comprendre le principe du filtrage médian je vous invite de consulter partie 1/3 du projet.
Résultats de simulation avec matlab
Simulation pour N=1
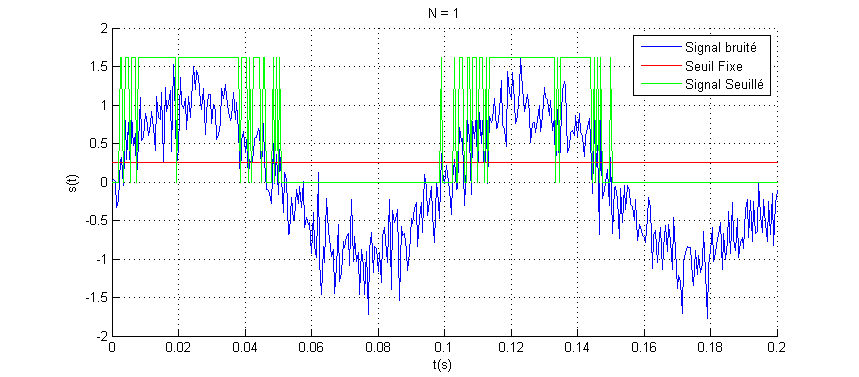
Simulation pour N varié de 4 à 16
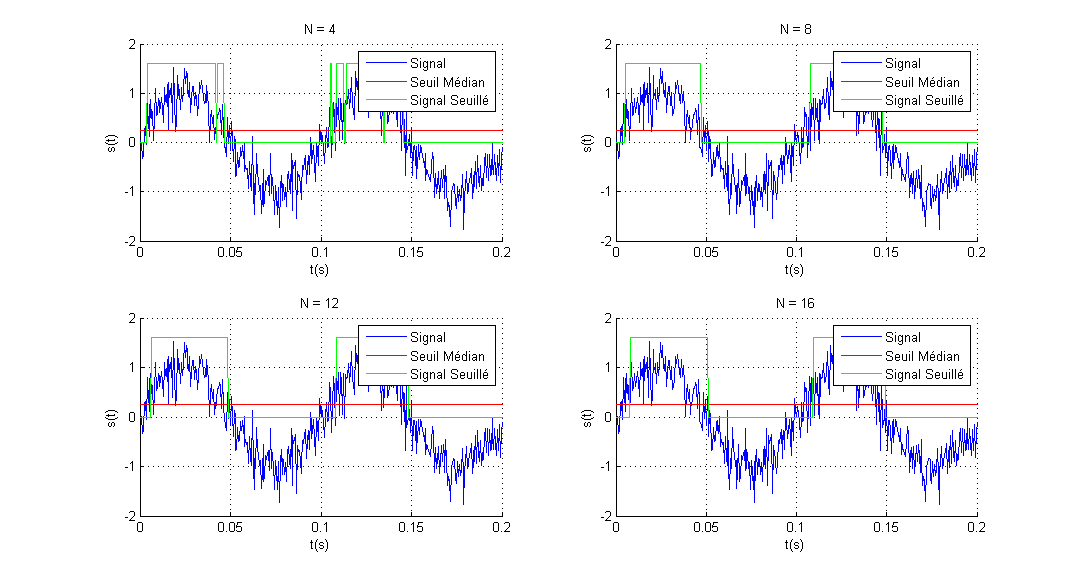
La qualité du seuillage s’améliore avec l’augmentation de la taille du filtre (A partir de N=8).
Comparaison entre le seuillage moyenné et le seuillage médian
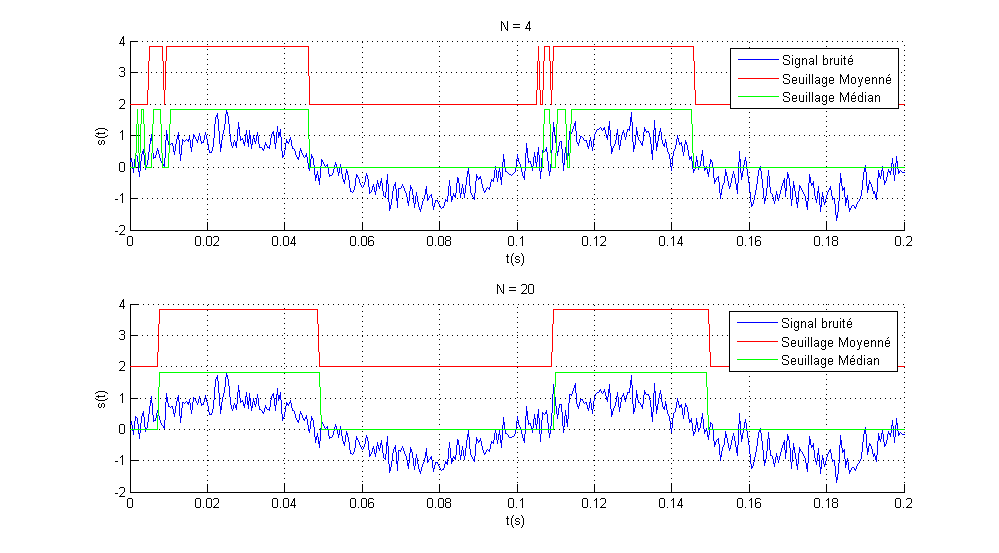 Visiblement il n’y a pas une différence en les deux techniques de seuillage. Les deux donnent de bons résultats à partir de N=8 échantillons pour un bruit normal d’une variance de 1/10 et un moyen nul aditionné à un signal sinusoïdal d’amplitude 1 et de valeur moyenne nulle.
Visiblement il n’y a pas une différence en les deux techniques de seuillage. Les deux donnent de bons résultats à partir de N=8 échantillons pour un bruit normal d’une variance de 1/10 et un moyen nul aditionné à un signal sinusoïdal d’amplitude 1 et de valeur moyenne nulle.
Le signal logique est décalé de 2 afin d’observer la différence entre les deux sorties logiques.
Programme Matlab
…
Suil_med = max(s_t)/4;
N_seuil_med =4:4:20;
s_seuil_med = zeros(length(N_seuil_med),length(s_t));
Mediane=0*s_t;
seuil_t=Suil_med*ones(1,length(s_t));
for k=1:length(N_seuil_med)
for i=N_seuil_med(k) :length(s_t)
% Calcul de la valeur dédiane du signal
s_b_sort = sort(s_b_t(i-N_seuil_med(k)+1:i));
Mediane(i)= s_b_sort(floor(N_seuil_med(k)/2.0));
% Application du seuil moyenné
if(Mediane(i)>=Suil_med )
s_seuil_med(k,i)=1*max(s_b_t);
end
% else
% s_seuil(i)=0;
% end
end
end
% Affichage
figure(4);
subplot(221);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_med(1,:),'g');
legend('Signal','Seuil Médian', 'Signal Seuillé');
title('N = 4');
subplot(222);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_med(2,:),'g');
legend('Signal','Seuil Médian', 'Signal Seuillé');
title('N = 8');
subplot(223);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_med(3,:),'g');
legend('Signal','Seuil Médian', 'Signal Seuillé');
title('N = 12');
subplot(224);
grid on ; hold on ;
xlabel('t(s)');
ylabel('s(t)');
plot(t,s_b_t,'b');
plot(t,seuil_t,'r');
plot(t,s_seuil_med(4,:),'g');
legend('Signal','Seuil Médian', 'Signal Seuillé');
title('N = 16');
************

4 réponses sur « Projet électronique : Traitement du signal avec Arduino # Lissage & Seuillage d’un signal 2/3 »
[…] Etude et simulation numérique du filtre Moyenneur avec Matlab [1/3] […]
good works , keep going
Thank you
good works, keep going